|
Be the first user to complete this post
|
Add to List |
297. Dijkstra's – Shortest Path Algorithm (SPT)
What is Dijkstra’s algorithm?
- Dijkstra algorithm is a greedy algorithm.
- It finds a shortest path tree for a weighted undirected graph.
- This means it finds the shortest paths between nodes in a graph, which may represent, for example, road networks
- For a given source node in the graph, the algorithm finds the shortest path between a source node and every other node.
- This algorithm is also used for finding the shortest paths from a single node to a single destination node by stopping the algorithm once the shortest path to the destination node has been determined.
- Dijkstra’s algorithm is very similar to Prim’s algorithm. In Prim’s algorithm, we create minimum spanning tree (MST) and in the Dijkstra algorithm, we create the shortest path tree (SPT) from the given source.
Example:
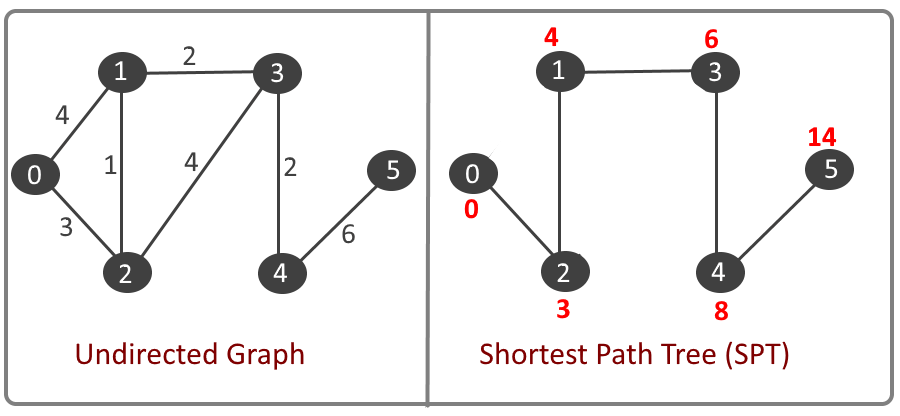
How to implement Dijkstra’s algorithm?
- Start with the empty Shortest Path Tree (SPT).
- Maintain a set SPT[] to keep track to vertices included in SPT.
- Assign a distance value to all the vertices, (say distance []) and initialize all the distances with +∞ (Infinity) except the source vertex. This will be used to keep track of distance of vertices from the source vertex. Distance of source vertex to source vertex will be 0.
- Repeat the following steps until all vertices are processed.
- Pick the vertex u which is not in SPT[] and has minimum distance.
- Add vertex u to SPT[].
- Loop over all the adjacent vertices of
- For adjacent vertex v, if v is not in SPT[] and distance[v] > distance[u] + edge u-v weight then update distance[v] = distance[u] + edge u-v weight
Please see the animation below for better understanding.
Ways to Implement:
- Adjacency Matrix – Searching.
- Adjacency List – Binary Heap
- Adjacency List – Priority Queue
- Adjacency List – TreeSet
Time Complexity:
The time complexity of Dijkstra algorithm depends on the data structures used for the graph and for ordering the edges by weight.
| Data Structure of Graph | Ordering | Time Complexity |
| Adjacency Matrix | Searching | O(|V|2) |
| Adjacency List | Binary Heap | O(|E|log|V|) |
| Adjacency List | Priority Queue | O(|E|log|V|) |
| Adjacency List | TreeSet | O(|E|log|V|) |
Usages:
- Dijkstra's algorithm can be used to find the shortest route between one city and all other cities.
- Shortest path algorithm is used in network routing protocols,
- IS-IS (Intermediate System to Intermediate System)
- Open Shortest Path First (OSPF).
Reference - Wiki

