|
Be the first user to complete this post
|
Add to List |
426. Check if Graph is Bipartite - Adjacency List using Depth-First Search(DFS)
Objective: Given a graph represented by the adjacency List, write a Depth-First Search(DFS) algorithm to check whether the graph is bipartite or not.
Earlier we have solved the same problem using Adjacency Matrix (Check if Graph is Bipartite - Adjacency Matrix) with Time complexity: O(V2) where V - No of vertices in the graph. In this article, we will solve it using the Adjacency List which will reduce the time complexity to O(V+E), where V - no of vertices and E - No of edges. Before we proceed, if you are new to Bipartite graphs, lets brief about it first
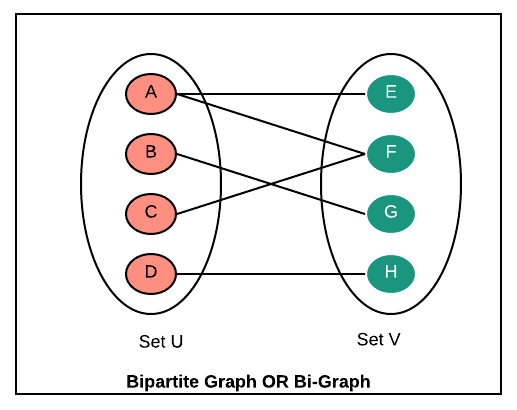
Bipartite Graphs OR Bigraphs is a graph whose vertices can be divided into two independent groups or sets so that for every edge in the graph, each end of the edge belongs to a separate group. There should not be any edge where both ends belong to the same set. Please read "Introduction to Bipartite Graphs OR Bigraphs".
Example:
Please read the following recommended articles before continue
Approach: Coloring of vertices - Check if Graph Two-Colorable
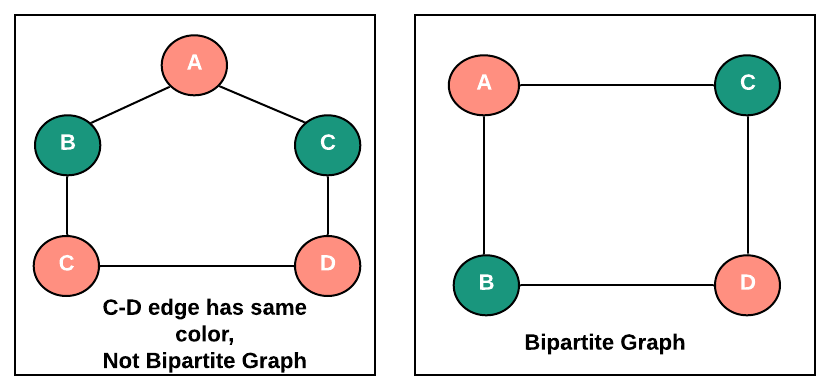
Choose three colors- RED, GREEN, WHITE. As you know in Bipartite graph, both ends of each edge belong to separate group, Let's say here two groups are RED and GREEN and for a graph to be bipartite, for each edge- one end has to be RED and another end has to be GREEN.
- Initially color all the vertices in WHITE and as algorithm advances, these vertices will be colored as RED or GREEN.
- Pick a vertex with color WHITE, now color it with RED. Now check all the neighbors of vertex. If these neighbors are in WHITE color, color these in GREEN, after that check neighbors of neighbors, If these neighbors are in WHITE color, color them in RED and so on, color the neighbors in alternate of RED and GREEN colors. Use Depth-First Search for this traversal.
- Do the step above until all the vertices are in either RED or GREEN color if that happens means graph is bipartite.
- During this process, if you find a neighbor vertex which is already colored in the same color as the current vertex or in other words you found an edge where both vertices are in the same color, stop the further process since the graph is not bipartite.
Time Complexity- O(V+E) where V - no of vertices and E - No of edges
Output:
Graph is Bipartite: false -------------------------- Graph is Bipartite: true

