This post is completed by 4 users

  • 2
 Add to List
Beginner

115. Graph Representation - Adjacency Matrix and Adjacency List

What is Graph:

G = (V,E)

Graph is a collection of nodes or vertices (V) and edges(E) between them. We can traverse these nodes using the edges. These edges might be weighted or non-weighted.

There can be two kinds of Graphs

  • Un-directed Graph - when you can traverse either direction between two nodes.
  • Directed Graph - when you can traverse only in the specified direction between two nodes.
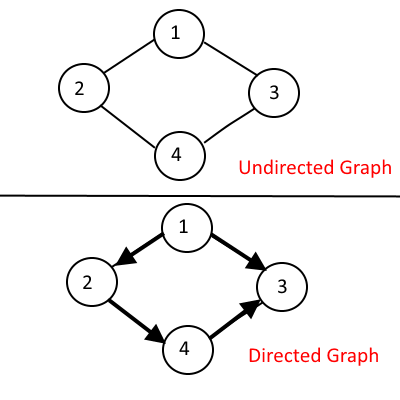
Directed and Undirected Graph

Now how do we represent a Graph, There are two common ways to represent it:

  • Adjacency Matrix
  • Adjacency List

Adjacency Matrix:

Adjacency Matrix is 2-Dimensional Array which has the size VxV, where V are the number of vertices in the graph. See the example below, the Adjacency matrix for the graph shown above.

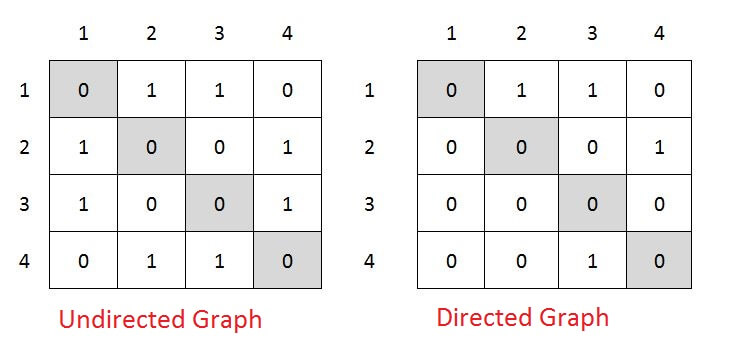
Adjacency Matrix

adjMaxtrix[i][j] = 1 when there is edge between Vertex i and Vertex j, else 0.

It's easy to implement because removing and adding an edge takes only O(1) time.

But the drawback is that it takes O(V2) space even though there are very less edges in the graph.

Adjacency List:

Adjacency List is the Array[] of Linked List, where array size is same as number of Vertices in the graph. Every Vertex has a Linked List. Each Node in this Linked list represents the reference to the other vertices which share an edge with the current vertex. The weights can also be stored in the Linked List Node.

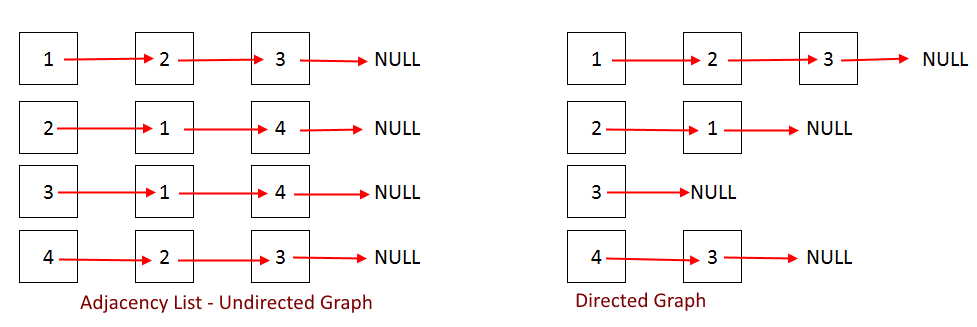
Adjacency List

The code below might look complex since we are implementing everything from scratch like linked list, for better understanding. Read the articles below for easier implementations (Adjacency Matrix and Adjacency List)

Output:

Nodes connected to Vertex 0 are :
  3  2  1
Nodes connected to Vertex 1 are :
  2
Nodes connected to Vertex 2 are :
  4

Related Problems: