|
Be the first user to complete this post
|
Add to List |
287. Kruskal's Algorithm – Minimum Spanning Tree (MST) - Complete Implementation
What is Kruskal Algorithm?
- Kruskal's algorithm for finding the Minimum Spanning Tree(MST), which finds an edge of the least possible weight that connects any two trees in the forest
- It is a greedy algorithm.
- It finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized.
- If the graph is not connected, then it finds a minimum spanning forest (a minimum spanning tree for each connected component).
- Number of edges in MST: V-1 (V – no of vertices in Graph).
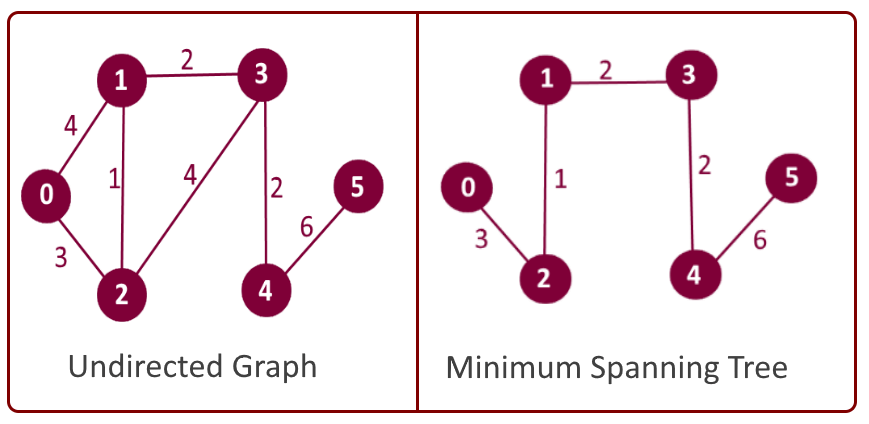
Example:
How this algorithm works?
We strongly recommend reading Find Cycle in Undirected Graph using Disjoint Set (Union-Find) before continue.
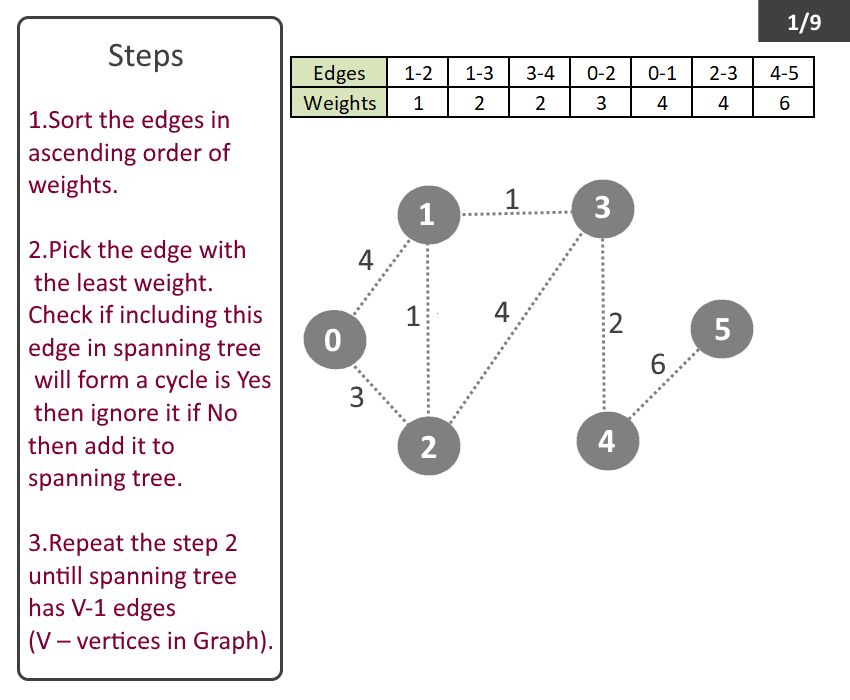
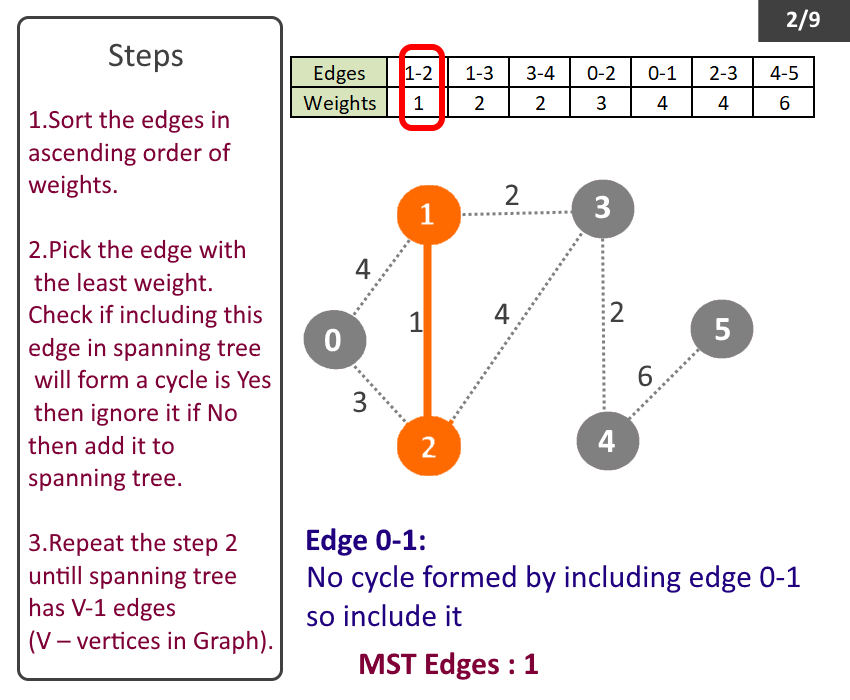
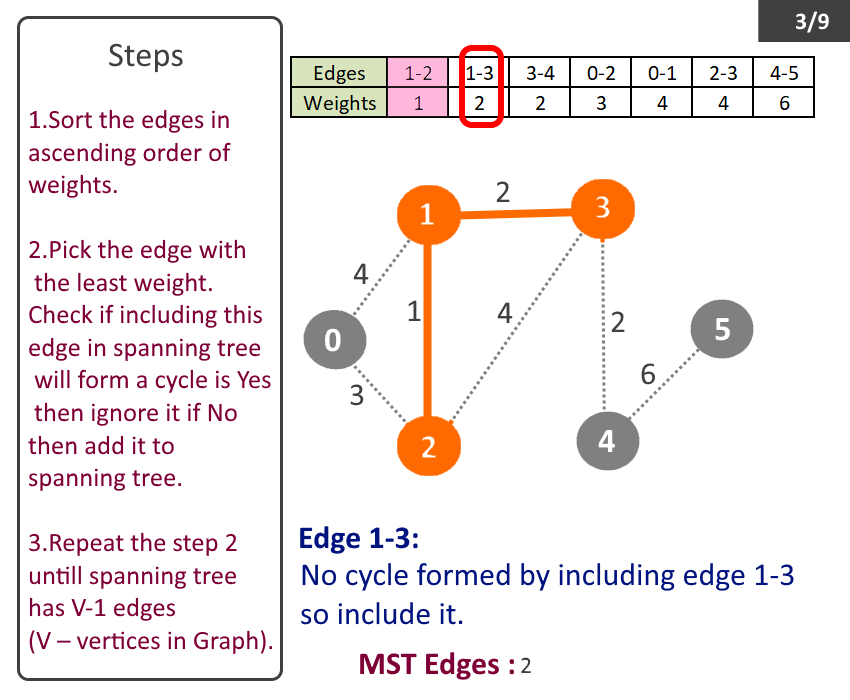
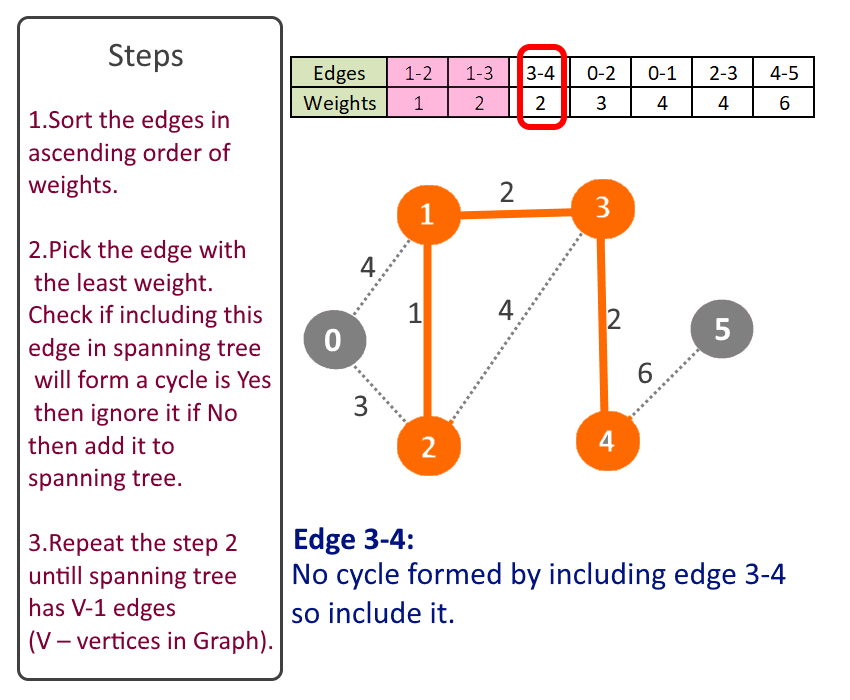
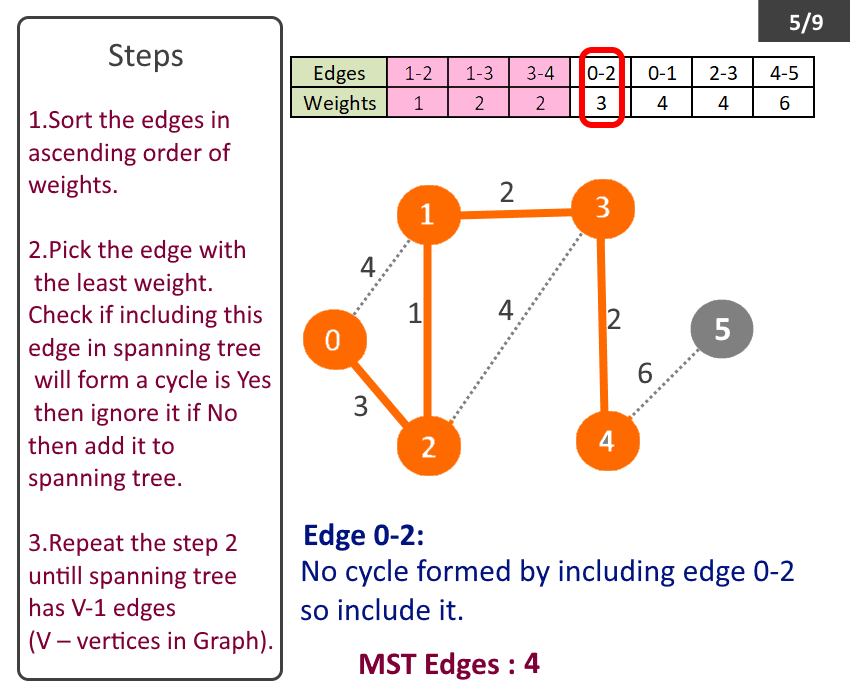
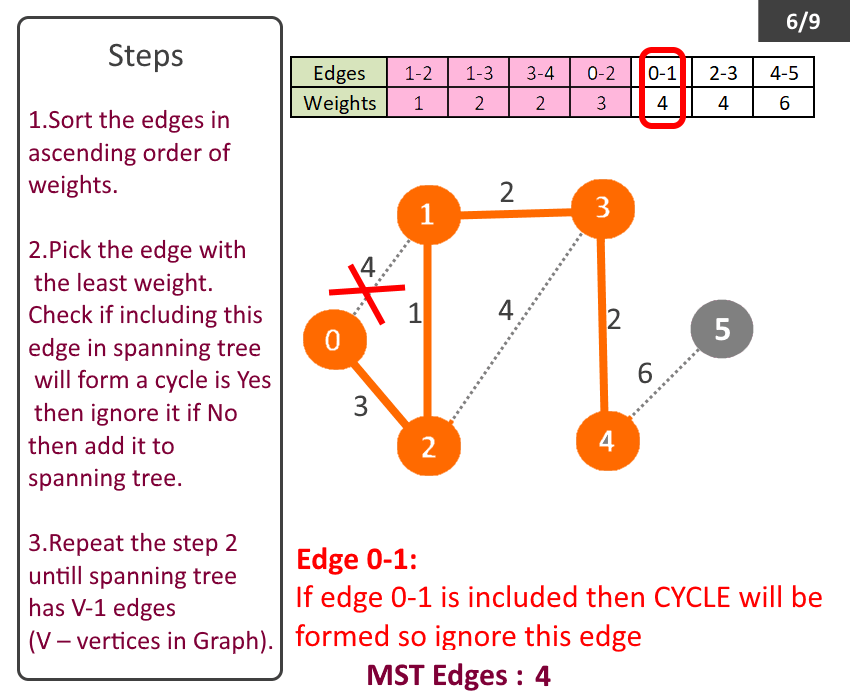
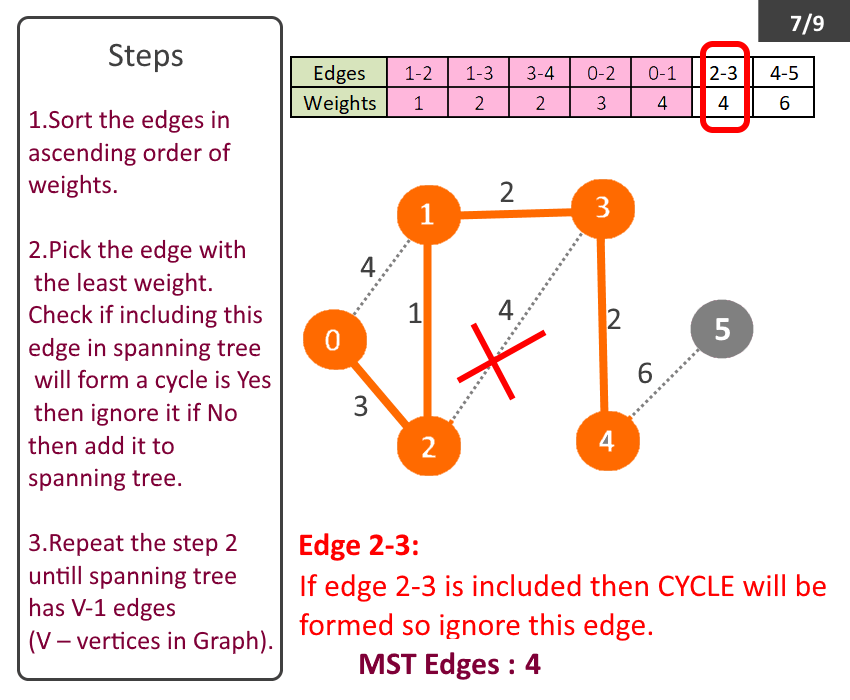
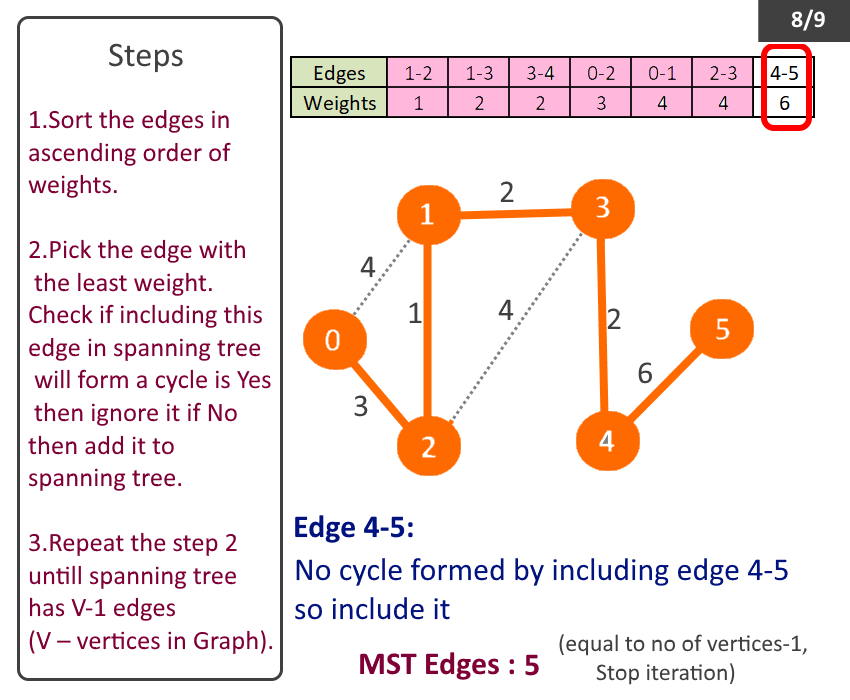
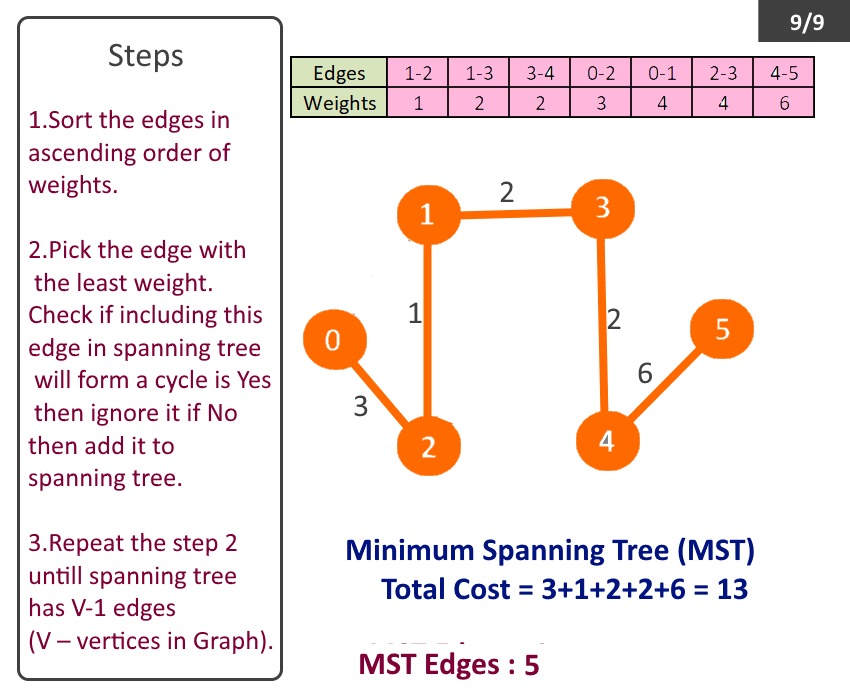
- Sort the edges in ascending order of weights.
- Pick the edge with the least weight. Check if including this edge in spanning tree will form a cycle is Yes then ignore it if No then add it to spanning tree.
- Repeat the step 2 till spanning tree has V-1 (V – no of vertices in Graph).
- Spanning tree with least weight will be formed, called Minimum Spanning Tree
Pseudo Code:
KRUSKAL(G):
A = ∅
foreach v ∈ G.V:
MAKE-SET(v)
foreach (u, v) in G.E ordered by weight(u, v), increasing:
if FIND-SET(u) ≠ FIND-SET(v):
A = A ∪ {(u, v)}
UNION(u, v)
return A
See the animation below for more understanding.
Output:
Minimum Spanning Tree: Edge-0 source: 1 destination: 2 weight: 1 Edge-1 source: 1 destination: 3 weight: 2 Edge-2 source: 3 destination: 4 weight: 2 Edge-3 source: 0 destination: 2 weight: 3 Edge-4 source: 4 destination: 5 weight: 6
Click here to read about - Minimum Spanning Tree using Prim's Algorithm
Reference - Wiki