This post is completed by 1 user

  • 0
 Add to List
Hard

334. Dijkstra Algorithm Implementation – TreeSet

Earlier we have seen what Dijkstra algorithm is and how it works. In this article, we will see its implementation using adjacency list and TreeSet.

brief: What is Dijkstra’s algorithm?

  • Dijkstra algorithm is a greedy algorithm.
  • It finds a shortest path tree for a weighted undirected graph.
  • This means it finds the shortest paths between nodes in a graph, which may represent, for example, road networks
  • For a given source node in the graph, the algorithm finds the shortest path between the source node and every other node.
  • This algorithm is also used for finding the shortest paths from a single node to a single destination node by stopping the algorithm once the shortest path to the destination node has been determined.
  • Dijkstra’s algorithm is very similar to Prim’s algorithm. In Prim’s algorithm, we create minimum spanning tree (MST) and in the Dijkstra algorithm, we create a shortest-path tree (SPT) from the given source.

Example:

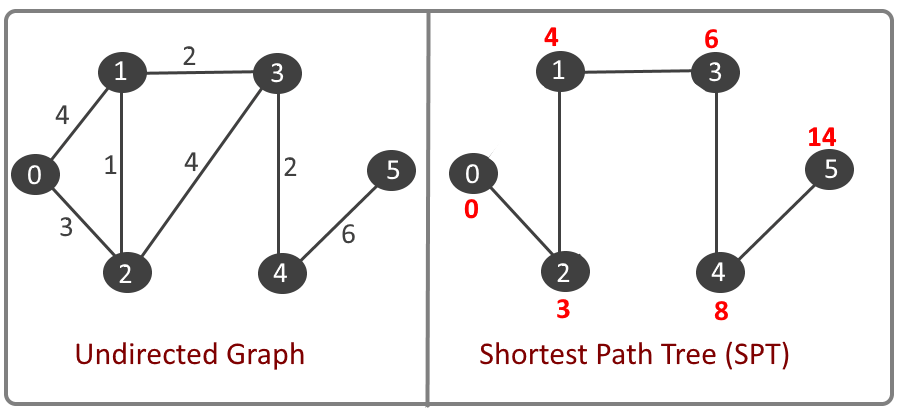
Dijkstra - Shortest Path Algorithm

Implementation – Adjacency List and Priority Queue

Prerequisites: Dijkstra Algorithm

Complete Algorithm:

  1. Will create a pair object for each vertex with two information, vertex and distance. (similar to heap node)
  2. Override the Comparator for TreeSet and sort them based on the key
  3. Use SPT[] to keep track of the vertices that are currently in the Shortest Path Tree(SPT).
  4. Create distance [] to keep track of the distance for each vertex from the source. , initialize all distances as MAX_VAL except the first vertex for which the distance will 0. (Start from the first vertex).
  5. Create a pair object for vertex 0 with distance 0 and insert it into the priority queue.
  6. while tree set is not empty
    1. Extract the min node from the tree set, say it vertex u, and add it to the SPT.
    2. For adjacent vertex v, if v is not in SPT[] and distance[v] > distance[u] + edge u-v weight then update distance[v] = distance[u] + edge u-v weight and add it to the tree set.

Total vertices: V, Total Edges : E

  • O(logV) – to extract each vertex from the queue. So for V vertices – O(VlogV)
  • O(logV) – each time a new pair object with a new key value of a vertex will be done for at most once for each edge. So for total E edge – O(ElogV)
  • So overall complexity: O(VlogV) + O(ElogV) = O((E+V)logV) = O(ElogV)

See the animation below for more understanding

 

Output:

Dijkstra Algorithm: (Adjacency List + TreeSet)

Source Vertex: 0 to vertex 0 distance: 0
Source Vertex: 0 to vertex 1 distance: 4
Source Vertex: 0 to vertex 2 distance: 3
Source Vertex: 0 to vertex 3 distance: 6
Source Vertex: 0 to vertex 4 distance: 8
Source Vertex: 0 to vertex 5 distance: 14

Related Problems: