This post is completed by 2 users

  • 0
 Add to List
Medium

171. Dynamic Programming - Longest Common Subsequence

Objective: Given two string sequences, write an algorithm to find the length of the longest subsequence present in both of them.

These kinds of dynamic programming questions are very famous in the interviews like Amazon, Microsoft, Oracle, and many more.

What is Longest Common Subsequence: The longest subsequence is a sequence that appears in the same relative order, but is not necessarily contiguous(not substring) in both string.

Example:

String A = "acbaed";
String B = "abcadf";

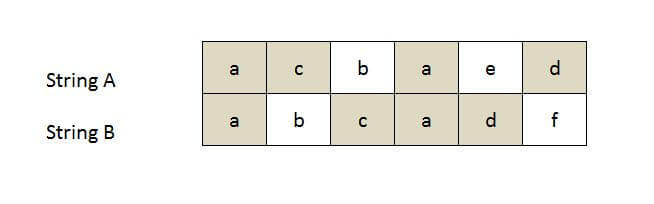
Longest Common Subsequence(LCS):     acad, Length: 4

Approach:

Recursion:

Start comparing strings in reverse order one character at a time.

Now we have 2 cases -

  1. Both characters are the same
    1. add 1 to the result and remove the last character from both the strings and make a recursive call to the modified strings.
  2. Both characters are different
    1. Remove the last character of String 1 and make a recursive call and remove the last character from String 2 and make a recursive and then return the max from returns of both recursive calls. see example below

Example:

Case 1: 

String A: "ABCD", String B: "AEBD"

LCS("ABCD", "AEBD") = 1 + LCS("ABC", "AEB")

Case 2: 

String A: "ABCDE", String B: "AEBDF"

LCS("ABCDE", "AEBDF") = Max(LCS("ABCDE", "AEBD"), LCS("ABCD", "AEBDF"))
 
LCS :4

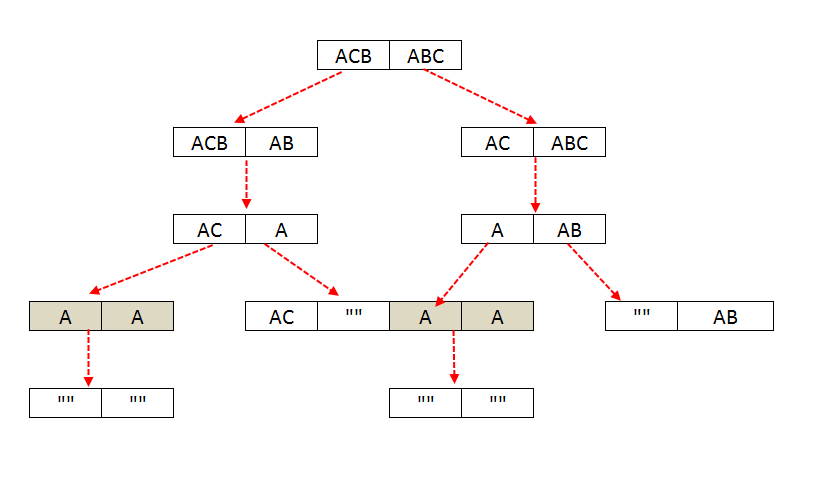
In a given string of length n, there can be 2n subsequences that can be made, so if we do it by recursion then Time complexity will O(2n) since we will be solving sub-problems repeatedly.

Dynamic Programming:

We will solve it Bottom-Up and store the solution of the subproblems in a solution array and use it whenever needed, This technique is called Memoization. See the code for a better explanation.

 
LCS :4

Print the Longest Common Subsequence:

Take a look into the LCS[][] used in the code

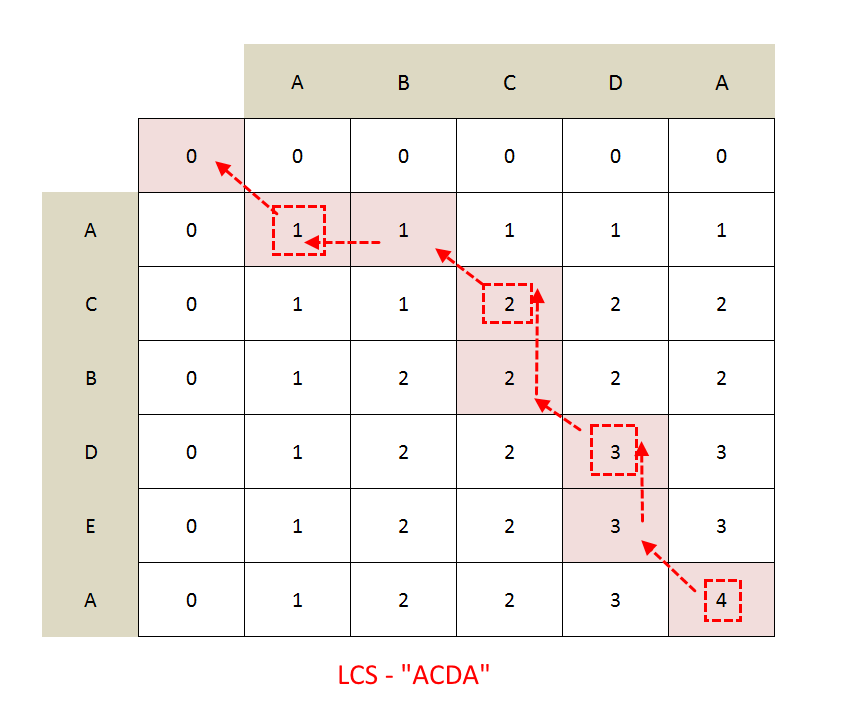
Start from bottom right corner and track the path and mark the cell from which cell the value is coming and whenever you go diagonal ( means last character of both string has matched, so we reduce the length of both the strings by 1, so we moved diagonally), mark those cells, this is our answer.

 
ACDA
 0 0 0 0 0 0
 0 1 1 1 1 1
 0 1 1 2 2 2
 0 1 2 2 2 2
 0 1 2 2 3 3
 0 1 2 2 3 3
 0 1 2 2 3 4
LCS :4

Click here to see the code for Dynamic Programming - Top Down Approach Java

Click here to see the code for Dynamic Programming - Top Down Approach Python

Related Problems: