Be the first user to complete this post

  • 0
 Add to List
Hard

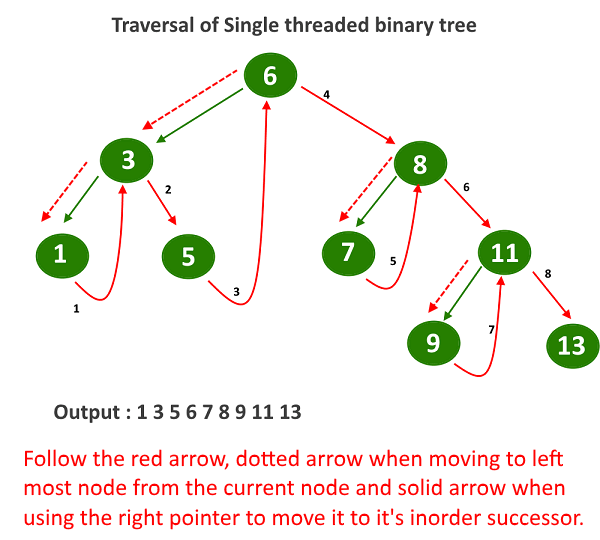
195. Single Threaded Binary Tree Complete Implementation

In an earlier article "Introduction to Threaded Binary Tree" we have seen what is a threaded binary tree, its types and what advantages it has over normal binary trees.

In this article, we will see the complete implementation of a single-threaded binary tree. ( Click here to read about “double threaded binary tree”)

Single threaded binary tree

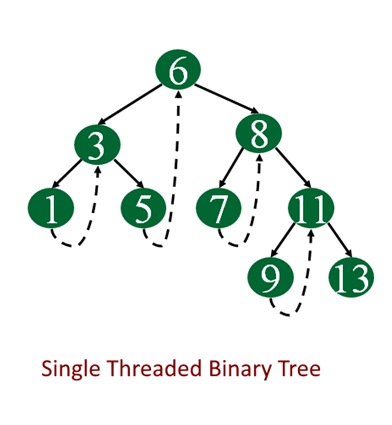
Image Source: http://web.eecs.umich.edu/~akamil/teaching/su02/080802.ppt

Single Threaded: each node is threaded towards either the in-order predecessor or successor (left or right) means all right null pointers will point to the in-order successor OR all left null pointers will point to the in-order predecessor.

Implementation:

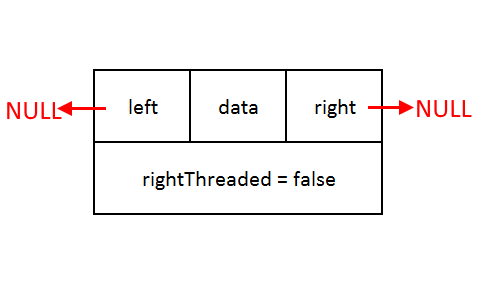
Let's see how the Node structure will look like

Node Structure of Single threaded binary tree
class Node{
    Node left;
    Node right;
    int data;
    boolean rightThread;
    public Node(int data){
        this.data = data;
        rightThread = false;
    }
}

In normal BST nodes we have left and right references and data but in the threaded binary tree we have a boolean in another field called "rightThreaded". This field will tell whether the node's right pointer is pointing to its in-order successor, but how, we will see it further.

Operations:

We will discuss two primary operations in a single-threaded binary tree

  1. Insert node into the tree
  2. Print or traverse the tree. ( here we will see the advantage of threaded tree)

Insert():

The insert operation will be quite similar to the Insert operation in the Binary search tree with few modifications.

  • To insert a node our first task is to find the place to insert the node.
  • Take cur­rent = root.
  • start from the cur­rent and com­pare root.data with n.
  • Always keep track of the parent node while moving left or right.
  • if current.data is greater than n that means we go to the left of the root, if after moving to left, the current = null then we have found the place where we will insert the new node. Add the new node to the left of the parent node and make the right pointer point to the parent node and rightThread = true for the new node.
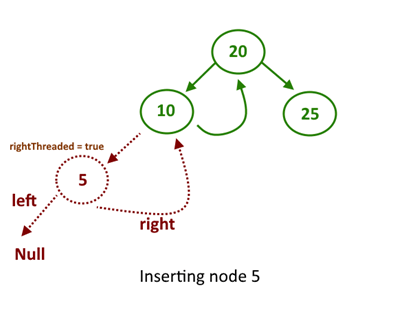
  • Insert Node into Single Threaded Binary Tree -1
  • if current.data is smaller than n that means we need to go to the right of the root, while going into the right subtree, check rightThread for the current node, which means the right thread is provided and points to the in order successor, if rightThread = false then and current reaches to null, just insert the new node else if rightThread = true then we need to detach the right pointer (store the reference, new node right reference will be a point to it)  of the current node and make it point to the new node and make the right reference point to stored reference. (See image and code for better understanding)
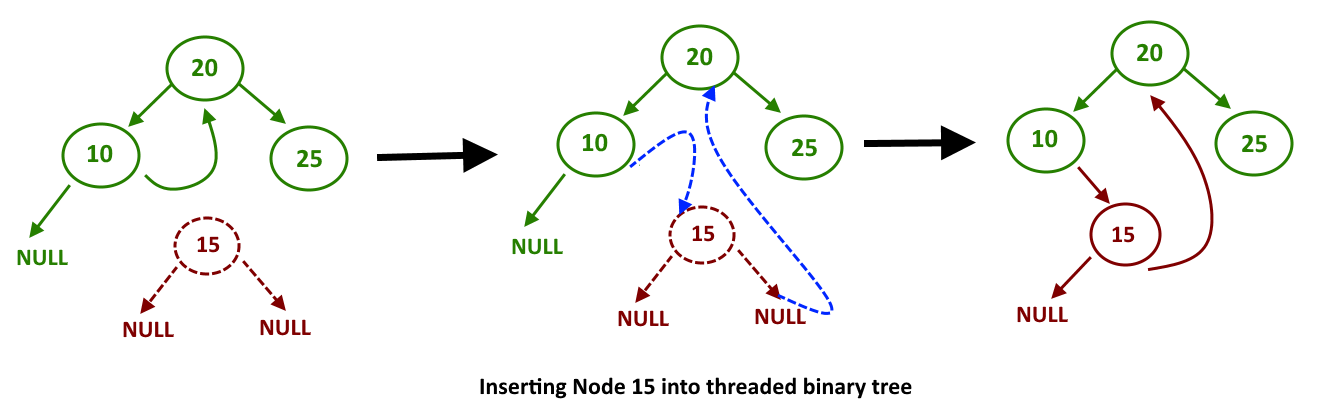
Insert Node into Single Threaded Binary Tree

Traverse():

traversing the threaded binary tree will be quite easy, with no need for any recursion or any stack for storing the node. Just go to the leftmost node and start traversing the tree using the right pointer and whenever rightThread = false again go to the leftmost node in the right subtree. (See image and code for better understanding)

 Traversal in Single Threaded Binary Tree-2 (1)

Output:

7 20 25 50 99 75 100

Related Problems: