|
This post is completed by 1 user
|
Add to List |
449. Check if Graph is Bipartite - Adjacency List using Breadth-First Search(BFS)
Objective: Given a graph represented by the adjacency List, write a Breadth-First Search(BFS) algorithm to check whether the graph is bipartite or not.
Earlier we have solved the same problem using Depth-First Search (DFS). In this article, we will solve it using Breadth-First Search(BFS). Before we proceed, if you are new to Bipartite graphs, lets brief about it first
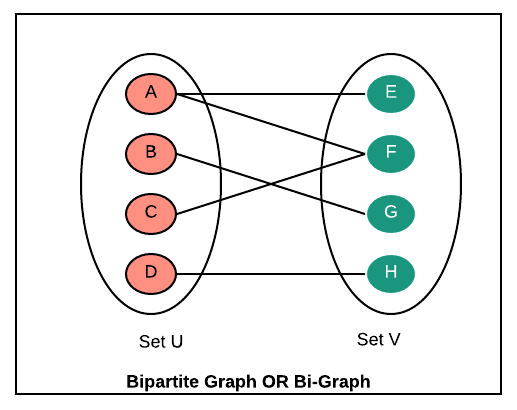
Bipartite Graphs OR Bigraphs is a graph whose vertices can be divided into two independent groups or sets so that for every edge in the graph, each end of the edge belongs to a separate group. There should not be any edge where both ends belong to the same set. Please read "Introduction to Bipartite Graphs OR Bigraphs".
Example:
Please read the following recommended articles before continue
Approach: Coloring of vertices - Check if Graph Two-Colorable using BFS
Choose three colors- RED, GREEN, WHITE. As you know in Bipartite graph, both ends of each edge belong to separate group, Let's say here two groups are RED and GREEN and for a graph to be bipartite, for each edge- one end has to be RED and another end has to be GREEN.
- Initially color all the vertices in WHITE and as algorithm advances, these vertices will be colored as RED or GREEN.
- Initialize queue.
- Pick a vertex with color WHITE, now color it with RED. Add it to the queue.
- While the queue is not empty
- take out a vertex from the queue. let's say its vertex v.
- Now check all the neighbors of vertex v.
- If these neighbors are in WHITE color, color them with the alternate color of vertex v means if v is RED, color the neighbors in GREEN and if v is GREEN, color the neighbors in RED. and add these neighbors in the queue.
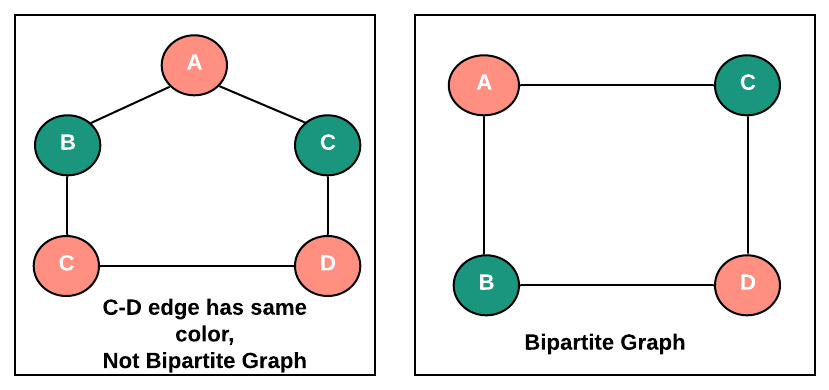
- If any of these neighbors are not in WHITE color, which means it was already colored earlier, check its color and if it has the same color as vertex v that means vertices connecting v and this neighbor cannot be in two colors means the graph is not bipartite. return false.
- Do steps 3 and 4 until all the vertices are in either RED or GREEN color if that happens means graph is bipartite.
Time Complexity- O(V+E)
Output:
Graph is Bipartite: false -------------------------- Graph is Bipartite: true

