|
This post is completed by 1 user
|
Add to List |
156. Backtracking - N Queens Problem
Objective: In chess, a queen can move as far as she pleases, horizontally, vertically, or diagonally. A chess board has 8 rows and 8 columns. The standard 8 by 8 Queen's problem asks how to place 8 queens on an ordinary chess board so that none of them can hit any other in one move.(Source: http://www.math.utah.edu/~alfeld/queens/queens.html)
Here we are solving it for N queens on the NxN chess board.
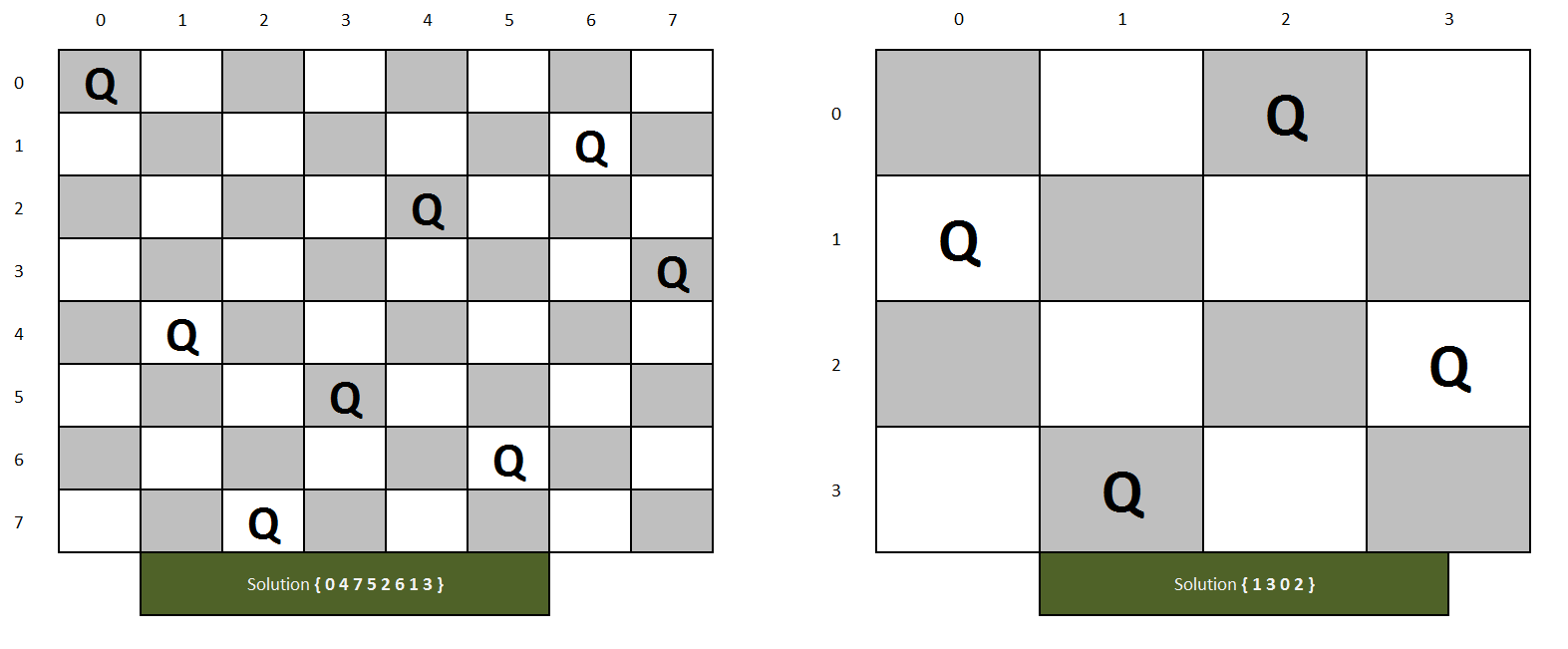
Approach: In this approach, we will see the basic solution with O(N^2) extra space we will improve it further to O(N) space. Click here to see the solution.
- Create a solution matrix of the same structure as a chess board.
- Whenever place a queen on the chess board, mark that particular cell in the solution matrix.
- At the end print the solution matrix, the marked cells will show the positions of the queens in the chess board.
Algorithm:
- Place the queen's column-wise, starting from the leftmost column
- If all queens are placed.
- return true and print the solution matrix.
- Else
- Try all the rows in the current column.
- Check if the queen can be placed here safely if yes mark the current cell in the solution matrix as 1 and try to solve the rest of the problem recursively.
- If placing the queen in the above step leads to the solution returning true.
- If placing the queen in the above step does not lead to the solution, BACKTRACK, mark the current cell in the solution matrix as 0, and return false.
- If all the rows are tried and nothing worked, return false and print NO SOLUTION.
Better Solution: If you notice in the solution matrix, at every row we have only one entry as 1, and the rest of the entries are 0. The solution matrix takes O(N2) space. We can reduce it to O(N). We will solve it by taking a one-dimensional array and considering solution[1] = 2 as "Queen at 1st row is placed at 2nd column. Click here to see the Better Solution.
Output:
0 0 1 0 1 0 0 0 0 0 0 1 0 1 0 0
Reference :
http://see.stanford.edu/materials/icspacs106b/H19-RecBacktrackExamples.pdf
http://www.geeksforgeeks.org/backtracking-set-3-n-queen-problem/

