|
This post is completed by 1 user
|
Add to List |
203. Dynamic Programming - Coin In a Line Game Problem
Objective: In this game, which we will call the coins-in-a-line game, an even number, n, of coins, of various denominations from various countries, are placed in a line. Two players, who we will call Alice and Bob, take turns removing one of the coins from either end of the remaining line of coins. That is, when it is a player’s turn, he or she removes the coin at the left or right end of the line of coins and adds that coin to his or her collection. The player who removes a set of coins with larger total value than the other player wins, where we assume that both Alice and Bob know the value of each coin.
Example:
coins [] = { 6, 9, 1, 2, 16, 8}
trial 1: (players will pick the best option available for them)
coins [] = { 6, 9, 1, 2, 16, 8} , Alice picks 8
coins [] = { 6, 9, 1, 2, 16}, Bob picks 16
coins [] = { 6, 9, 1, 2}, Alice picks 6
coins [] = { 9, 1, 2}, Bob picks 9
coins [] = {1, 2}, Alice picks 2
coins [] = {1}, Bob picks 1
Alice: 8+6+2 =16 Bob: 16+9+1=26 => Alice Lost
So clearly picking up the best in each move is not good for Alice. What else Alice can do to win the game.
trial 2: (Alice thinks about Bob's move, Will discuss the strategy in solution)
coins [] = { 6, 9, 1, 2, 16, 8} , Alice picks 6
coins [] = { 9, 1, 2, 16, 8}, Bob picks 9
coins [] = { 1, 2, 16, 8}, Alice picks 1
coins [] = 2, 16, 8}, Bob picks 8
coins [] = {2, 16}, Alice picks 16
coins [] = {2}, Bob picks 2
Alice: 6+1+16 =23 Bob: 9+8+2=19 => Alice Won
So this time Alice has won. Let's see the solution and discuss what Alice has done to win the game.
Approach:
We will solve this problem using Dynamic programming in a Bottom-up manner.
In the example above we have seen that in trial 1 Alice lost and in trial 2 Alice won. So clearly picking the best coin available in each move is a good option for Alice.
So the question is what Alice has done differently to win in the second trial. Since Alice and Bob, both are playing to win the game and both are equally clever then "Alice has to think about Bob's move means options available for Bob once Alice is done with the move, What Bob will pick (Bob is equally clever and tries to leave Alice with minimum values to be chosen from) and then what Alice will choose."
So if we can clearly see that each player is making the move by keeping in mind the two moves can be made in the future and pick the best of them.
Let's make it more clear- Suppose we have coins lined up from Ci to Cj wit the values of Vi to Vj respectively.
MV(i, j) = maximum value Alice can collect from i'th coin to j'th coin.
In every move, Alice has 2 options -
- Either pick the ith coin (from starting)
- OR pick the jth coin ( from the end).
Let's discuss both the options
Alice Picks the ith coin (from starting)

As we can see above if Alice picks the ith coin, Ci then Bob will be left with 2 choices Ci+1 and Cj, since Bob is equally clever Bob will pick the coin which will leave Alice with minimum value coins.
So if Bob picks i+1th coin then it will again Alice turn and the problem will be reduced to Alice having to pick a coin from i+2th to jth coin and similarly if Bob picks jth coin then it will again Alice turn and the problem will be reduced to Alice has to pick a coin from i+1th to j-1th coin.
So Alice will collection will be
= Vi + Min{MV(i+2,j), MV(i+1, j-1)}
Alice Picks the jth coin (from the end)
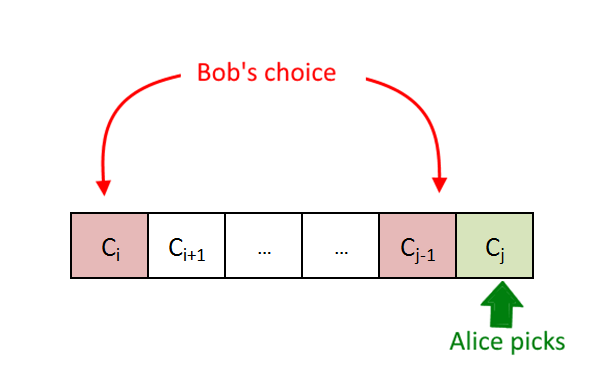
As we can see above if Alice picks the jth coin, Cj then Bob will be left with 2 choices Ci and Cj-1, since Bob is equally clever, Bob will pick the coin which will leave Alice with minimum value coins.
So if Bob picks ith coin then it will again Alice turn and the problem will be reduced to Alice has to pick a coin from i+1th to j-1th coin and similarly if Bob picks j-1th coin then it will again Alice turn and the problem will be reduced to Alice has to pick a coin from ith to j-2th coin.
So Alice will collection will be
= Vj + Min{MV(i+1,j-1), MV(i, j-2)}
So now we need to decide whether Alice should pick the ith coin or the jth coin. Alice will pick the coin which ever gives the more value considering 2 moves ahead
so
MV(i, j) = Max {Vi + Min{MV(i+2,j), MV(i+1, j-1)} , Vj + Min{MV(i+1,j-1), MV(i, j-2)}}
Let's see how the recursive equation will look like:

Output:
Max value pick up by player1(Alice)- 23
Reference: http://www.geeksforgeeks.org/dynamic-programming-set-31-optimal-strategy-for-a-game/

