Introduction to Minimum Spanning Tree (MST)

What is a Spanning Tree?

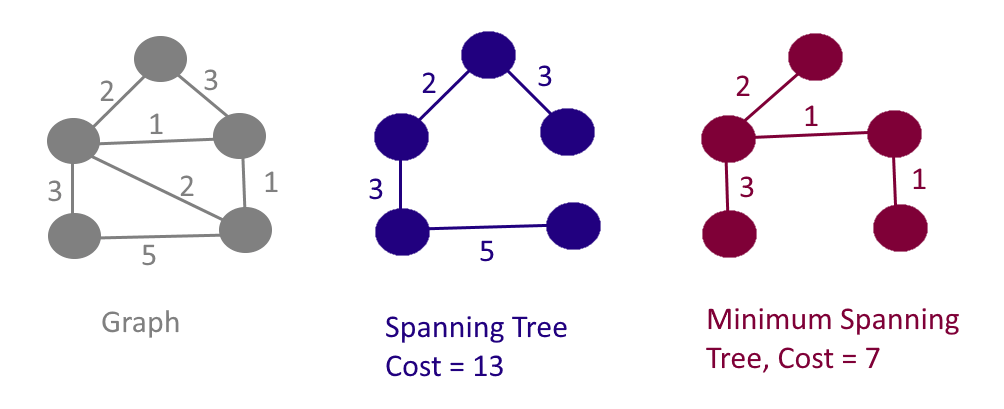
In an undirected and connected graph G=(V,E), a spanning tree is a subgraph that is a tree which includes all of the vertices of G, with minimum possible number of edges. A graph may have several spanning trees. The cost of the spanning tree is the sum of the weights of all the edges in the tree

What is a Minimum Spanning Tree?

A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted (un)directed graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible. Number of edges in MST: V-1 (V – no of vertices in Graph).

Example:

Algorithms for finding the Minimum Spanning Tree:

• Kruskal’s Algorithm
• Prim’s Algorithm

Applications:

Minimum spanning trees have direct applications in the design of networks, including computer networks, telecommunications networks, transportation networks, water supply networks, and electrical grids. Also used in

1. Approximating travelling salesman problem
2. Approximating multi-terminal minimum cut problem
3. Approximating minimum-cost weighted perfect Cluster Analysis
4. Handwriting recognition
5. Image segmentation
6. Circuit design

Reference - wiki

Also Read:

- Check if Graph is Bipartite - Adjacency List using Depth-First Search(DFS) Hard
- Number of Islands Medium
- Graph Representation - Adjacency Matrix and Adjacency List Beginner
- Implement Graph Using Map - Java Medium
- Disjoint Set Data Structure - Union Find Algorithm Hard
- Dijkstra’s – Shortest Path Algorithm (SPT) – Adjacency List and Min Heap – Java Implementation Hard
- Print All Paths in Dijkstra's Shortest Path Algorithm Hard
- Prim’s – Minimum Spanning Tree (MST) |using Adjacency List and Priority Queue with decrease key Hard