|
This post is completed by 1 user
|
Add to List |
428. Collatz Conjecture - Maximum Steps takes to transform (1, N) to 1.
Objective: Given a number N, write an algorithm to find the maximum number of steps it takes to transform (1, N) to 1 using Collatz Conjecture.
The Collatz conjecture is a conjecture in mathematics which states that no matter what value of Positive Number N, If the below sequence is followed then the sequence will always reach 1.
- If N is even, then do N = N/2
- If N is odd then do N = 3*N+1
- If N is 1 then stop else keep performing step 1 and step 2.
Recommended Article - Collatz Conjecture
Example:
N = 7 Max Steps needed to transform (1, 7 ) to 1: 16
Explanation: 1 Total Steps to transform N = 1 to 1: 0 2->1 Total Steps to transform N = 2 to 1: 1 3->10->5->16->8->4->2->1 Total Steps to transform N = 3 to 1: 7 4->2->1 Total Steps to transform N = 4 to 1: 2 5->16->8->4->2->1 Total Steps to transform N = 5 to 1: 5 6->3->10->5->16->8->4->2->1 Total Steps to transform N = 6 to 1: 8 7->22->11->34->17->52->26->13->40->20->10->5->16->8->4->2->1 Total Steps to transform N = 7 to 1: 16 8->4->2->1
Approach: Recursion
Solve for all the numbers from 1 to N using Collatz Conjecture and find no of steps taken by each number to transform to 1 and pick the maximum steps among those.
Output:
Max Steps needed to transform (1, 7 ) to 1: 16 Max Steps needed to transform (1, 6 ) to 1: 8
The problem with the above solution is that there are many overlapping subproblems, for example, if you solve for N = 4 , then the sequence will be 4, 2, 1 and for N = 8, the sequence will be 8, 4, 2, 1 that means you will be solving for numbers 4, 2, 1 again when you solve for N =8. we have a recursive equation and overlapping subproblems so this problem is a very good candidate for Dynamic programming. See the diagram below
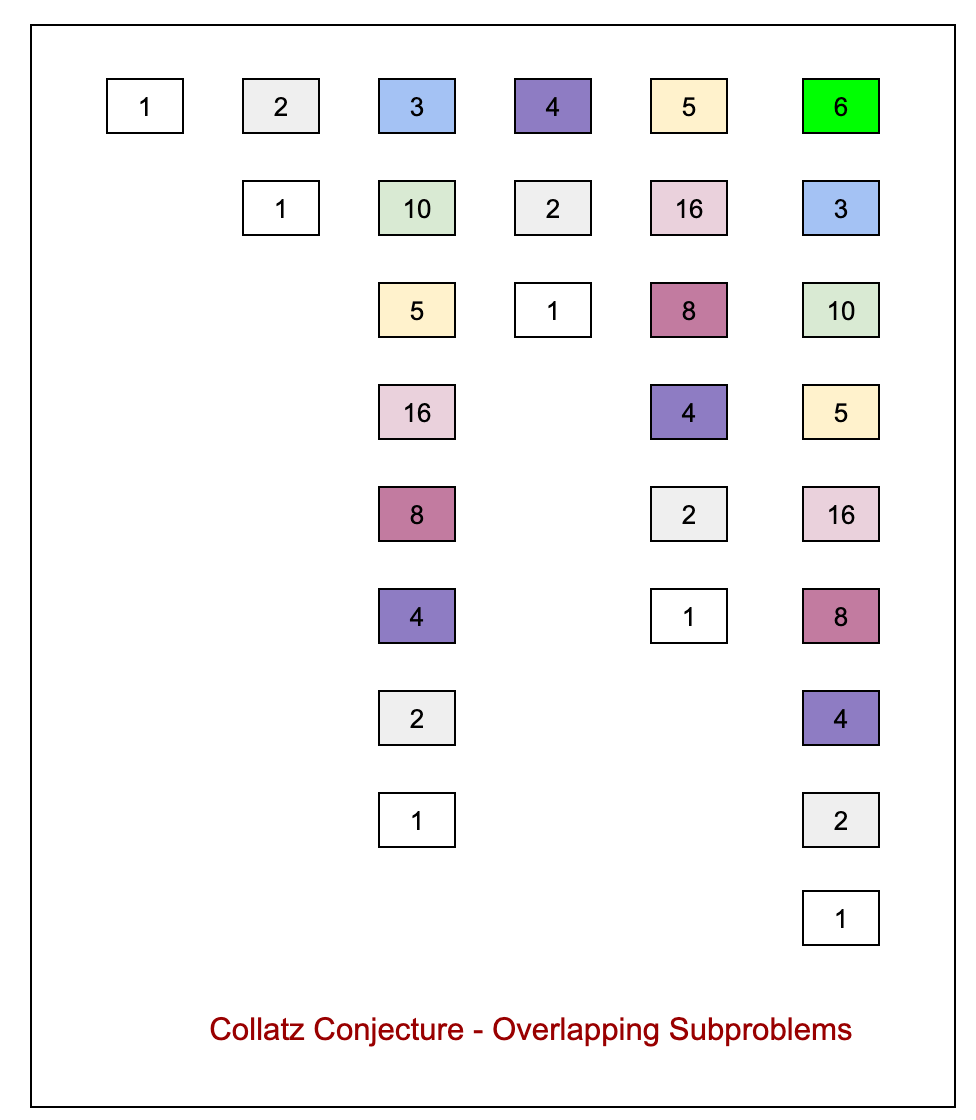
Approach - Dynamic Programming - Top-Down Approach
Have HashMap with Number as key and Steps as value and before making every recursive call for N, check if exist in the map if yes, use it else solve it and put it in the map for further uses.
Time Complexity: O(N)
Code:
Output:
Max Steps needed to transform (1, 7 ) to 1: 16 Max Steps needed to transform (1, 6 ) to 1: 8

