This post is completed by 1 user

  • 0
 Add to List
Medium

363. Evaluation of Infix expressions

Infix notation is commonly used in arithmetic formula or statements, the operators are written in-between their operands.

Let's assume the below

  • Operands are real numbers.
  • Permitted operators: +,-, *, /, ^(exponentiation)
  • Blanks are permitted in expression.
  • Parenthesis are permitted

Example:

A * ( B + C ) / D
2 * (5 + 3) / 4

Output: 4

Approach: Use Stacks

We will use two stacks

  • Operand stack: This stack will be used to keep track of numbers.
  • Operator stack: This stack will be used to keep operations (+, -, *, /, ^)

Order of precedence of operations-

  1. ^ (Exponential)
  2. / *
  3. + -

Note: brackets ( ) are used to override these rules.

Let's define the Process: (will be used for the main algorithm)

  1. Pop-out two values from the operand stack, let's say it is A and B.
  2. Pop-out operation from operator stack. let's say it is ‘+'.
  3. Do  A + B and push the result to the operand stack.

Algorithm:

Iterate through given expression, one character at a time

  1. If the character is an operand, push it to the operand stack.
  2. If the character is an operator,
    1. If the operator stack is empty then push it to the operator stack.
    2. Else If the operator stack is not empty,
      • If the character's precedence is greater than or equal to the precedence of the stack top of the operator stack, then push the character to the operator stack.
      • If the character's precedence is less than the precedence of the stack top of the operator stack then do Process (as explained above) until character's precedence is less or stack is not empty.
  3. If the character is "(", then push it onto the operator stack.
  4. If the character is ")", then do Process (as explained above) until the corresponding "(" is encountered in operator stack. Now just pop out the "(".

Once the expression iteration is completed and the operator stack is not empty, do Process until the operator stack is empty.  The values left in the operand stack is our final result.

Please see the walkthrough of an example below for more understanding.

 

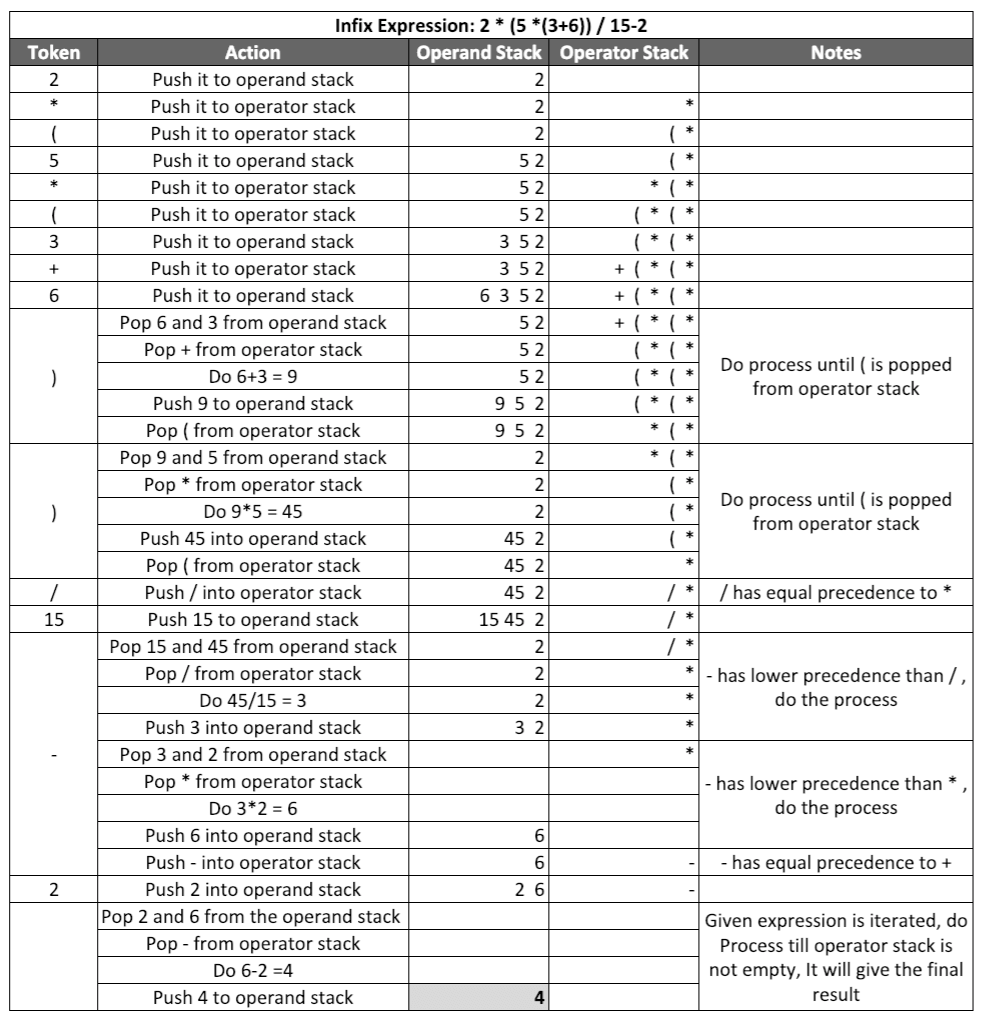
Output:

4

Related Problems: