|
This post is completed by 1 user
|
Add to List |
489. The number of cycles in a given array of integers.
Objective: Given an array of size N which contains integers from range 0 to N-1. (No duplicates). Write a program to find the number of cycles in the array.
Cycles in Array: Since the array is of size N and elements are from 0 to N-1 without any duplicates means all the elements appear exactly once. Create a graph with n vertices. Create an edge from vertex Vi to Vj if the element at position i should be in position j in the sorted ordering, With the logic above find the number of cycles in the given array. See the image below for better understanding.
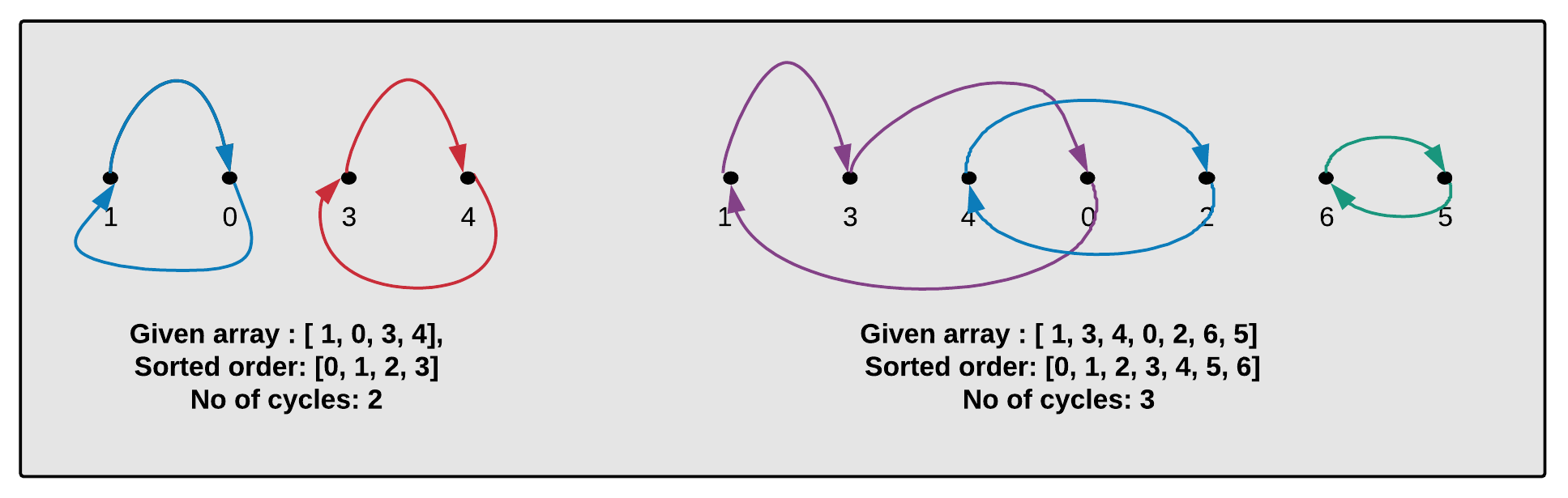
Example:
Given Array : [3, 2, 1, 0] Number of cycles: 2 Given Array : [2, 0, 1] Number of cycles: 1 Given Array : [1, 3, 4, 0, 2, 6, 5] Number of cycles: 3
Approach: Use DFS
- Create a visited[] to check if the array element is already visited.
- Initialize NoOfCycles = 0.
- Now iterate through input[] created in step 1, for each index i.
- If input[i] != i
- If i is not already visited then mark i as visited and jump to the next index which is at the index = input[i]. For example (1, 0) and i = 0 then jump to index=1. Repeat this process until you find an index which is already visited.
- NoOfCycles++.
- If input[i] != i
- Return NoOfCycles.
Walk-through:walk-through:
Input[] = [3, 2, 1, 0]
visited = [false, false, false, false]
NoOfCycles = 0
Index = 0, element = 3
0!=3 and 3 is not visited.
Mark 3 visited.
Jump to index = 3, element = 0
element 0 is not visited
Mark 0 visited.
Jump to index = 0, element = 3
3 is already visited.
NoOfCycles = 1
visited = [true, false, false, true]
Index = 1, process element = 2
1!=2 and 2 is not visited.
Mark 2 visited.
Jump to index = 2, element = 1
element 1 is not visited
Mark 1 visited.
Jump to index = 1, element = 2
2 is already visited.
NoOfCycles = 2
visited = [true, true, true, true]
NoOfCycles = 2
Output:
Given Array : [3, 2, 1, 0] No of cycles: 2
Given Array : [2, 0, 1] No of cycles: 1
Given Array : [1, 3, 4, 0, 2, 6, 5] No of cycles: 3

