|
This post is completed by 5 users
|
Add to List |
41. Sorted Array to Binary Search Tree of Minimal Height
Objective: Given a sorted array with unique elements, Create a binary search tree with minimal height.
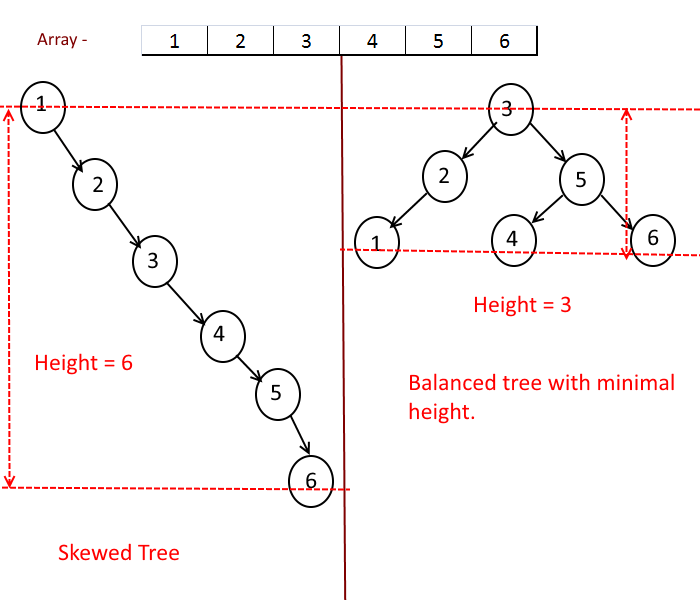
Why minimal height is important :
We can do the linear scan to the array and make the first element as root and insert all other elements into the tree but in that case tree will be skewed , which means all the nodes of the tree will be on the one side of the root so the height of the tree will be equal to the number of elements in the array. So here our objective is to keep the tree balanced as much as possible.
What is balanced Tree: A balanced tree is a tree in which difference between heights of sub-trees of any node in the tree is not greater than one. To read more about balanced tree, click here
Input: A one dimensional array
Output: Binary Search Tree of Minimal Height
Example:
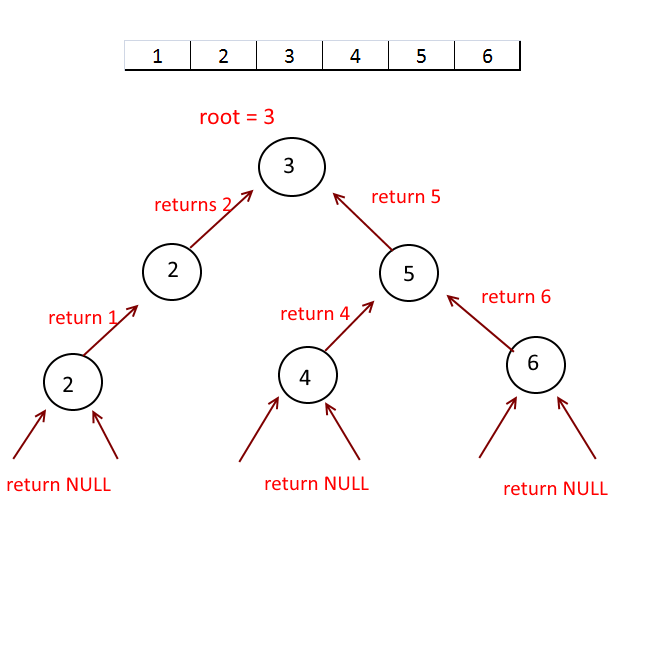
Approach - Recursion:
- Get the middle of the array
- make it a root. (By doing this we will ensure that half of the elements of the array will be on the left side of the root and half on the right side.)
- Take the left half of the array, call recursively, and add it to the left of the root.
- Take the right half of the array, call recursively add it to the right of the root.
- return root.
Output:
Tree Display : 2 3 6 7 8 9 12 15 16 18 20