Be the first user to complete this post

  • 0
 Add to List
Hard

Kruskal's Algorithm – Minimum Spanning Tree (MST) - Complete Java Implementation

What is Kruskal Algorithm?

  • Kruskal's algorithm for finding the Minimum Spanning Tree(MST), which finds an edge of the least possible weight that connects any two trees in the forest
  • It is a greedy algorithm.
  • It finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized.
  • If the graph is not connected, then it finds a minimum spanning forest (a minimum spanning tree for each connected component).
  • Number of edges in MST: V-1 (V – no of vertices in Graph).

Example:

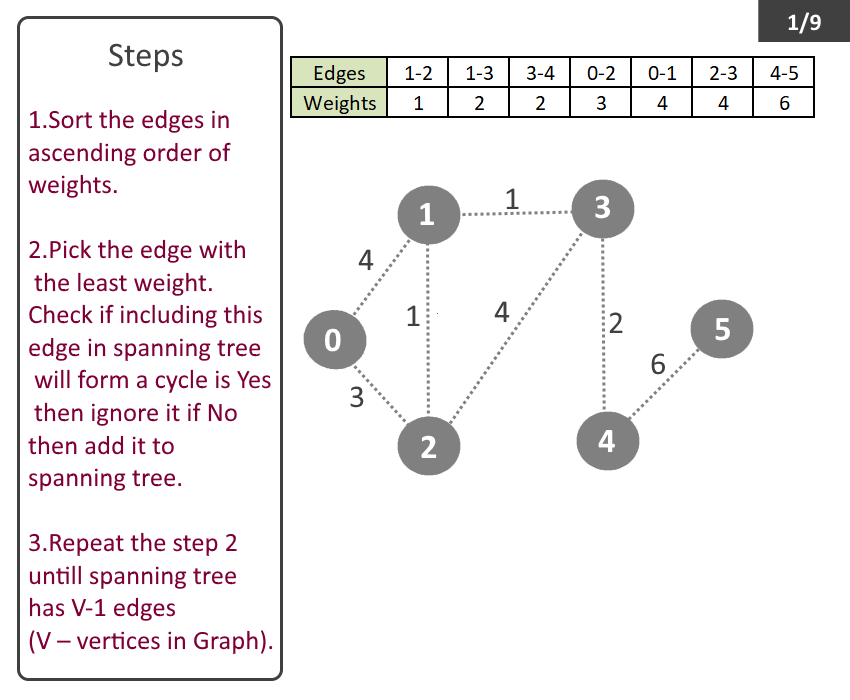
Minimum Spanning Tree (MST) Example

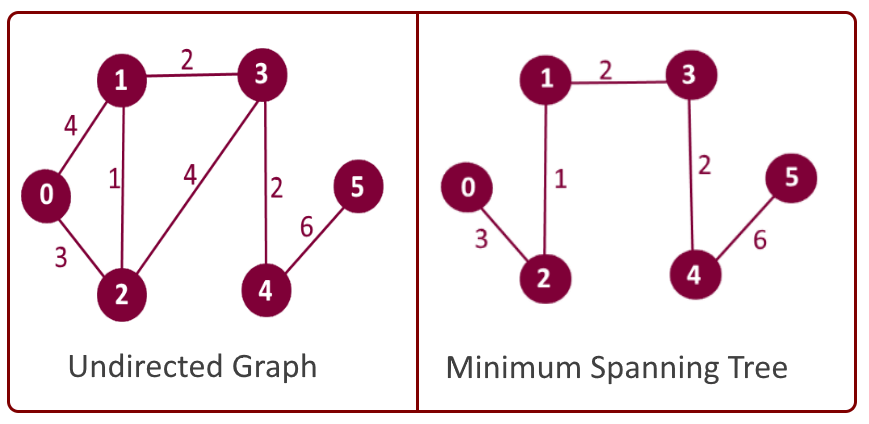
How this algorithm works?

We strongly recommend reading Find Cycle in Undirected Graph using Disjoint Set (Union-Find) before continue.

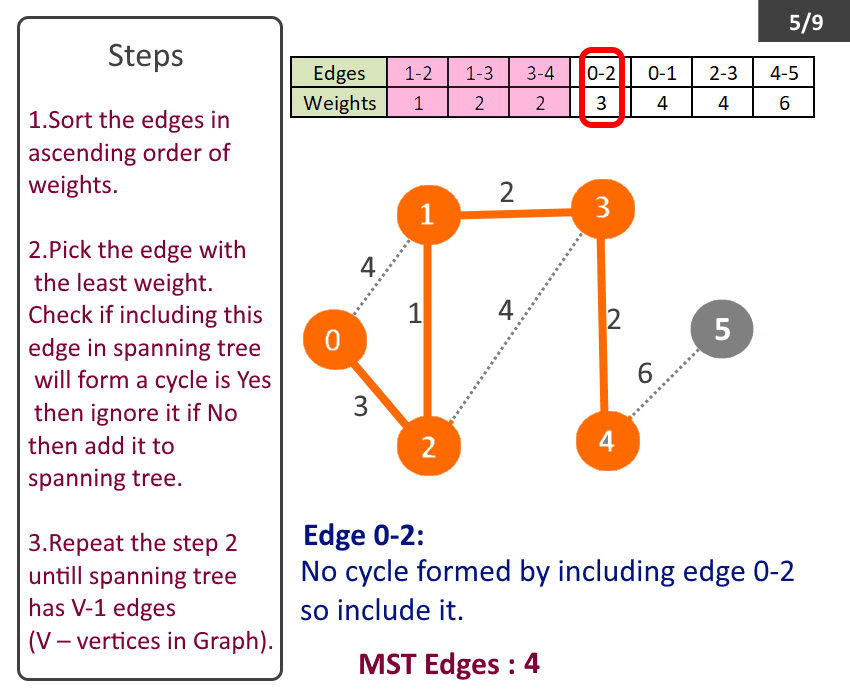
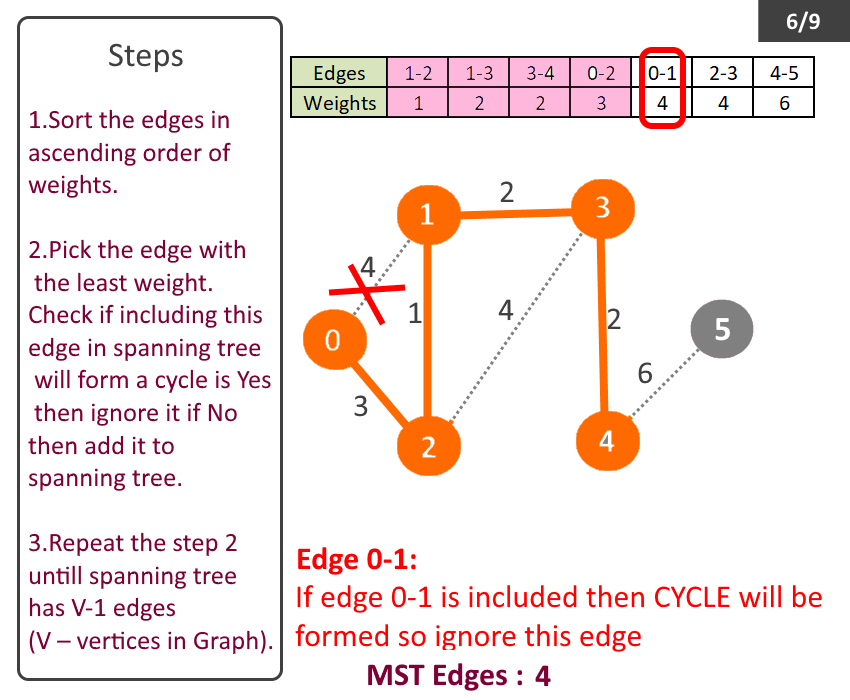
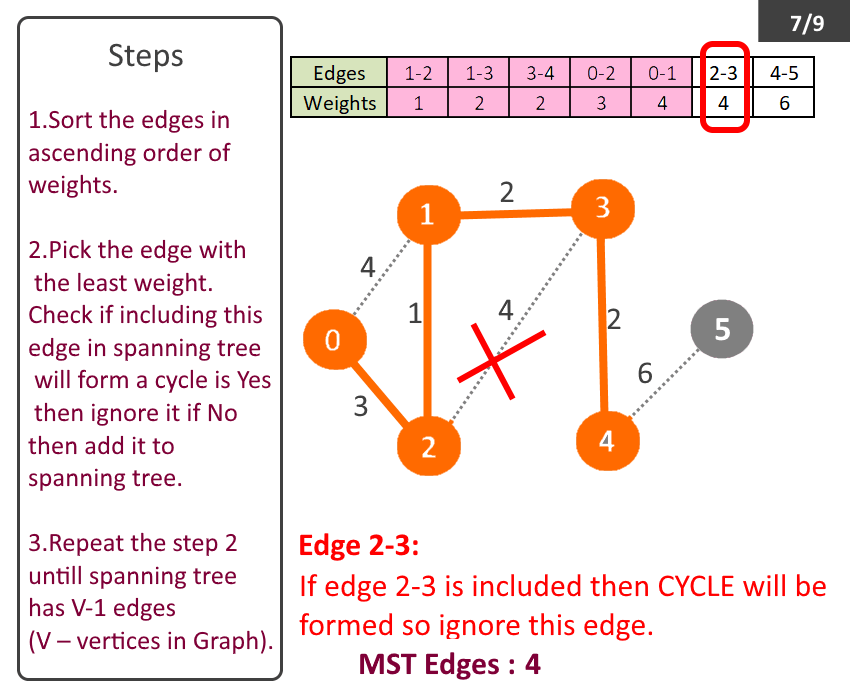
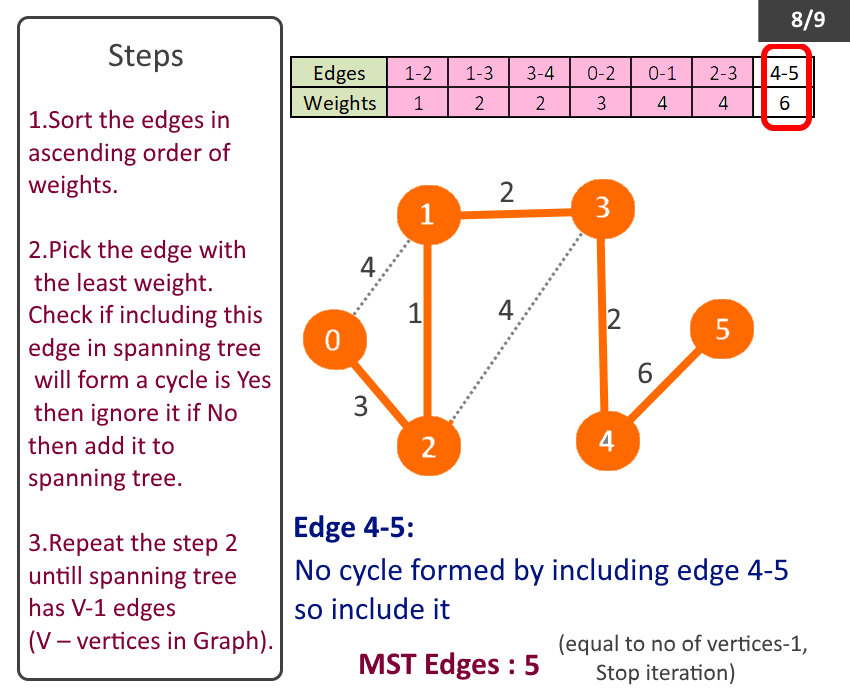
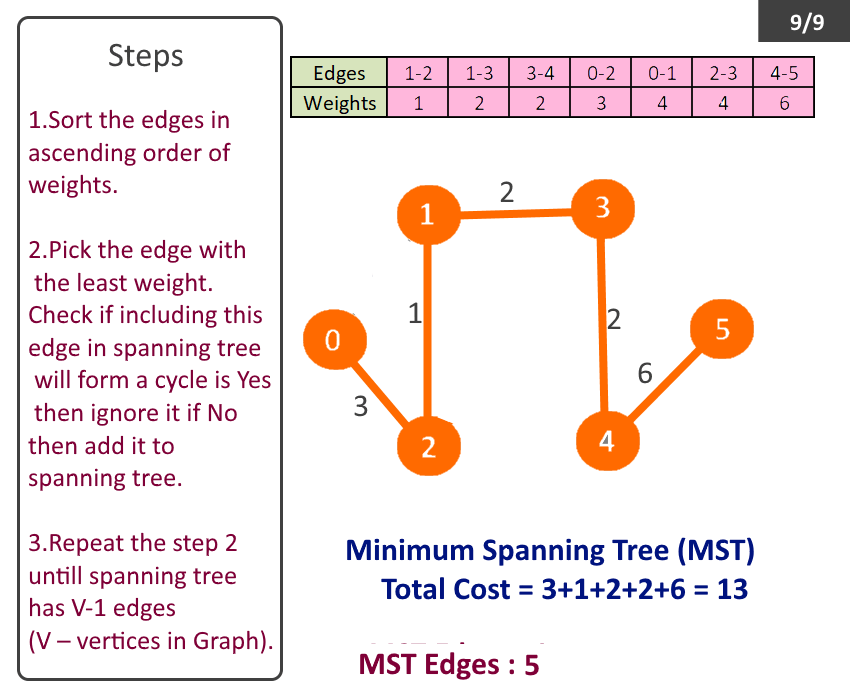
  1. Sort the edges in ascending order of weights.
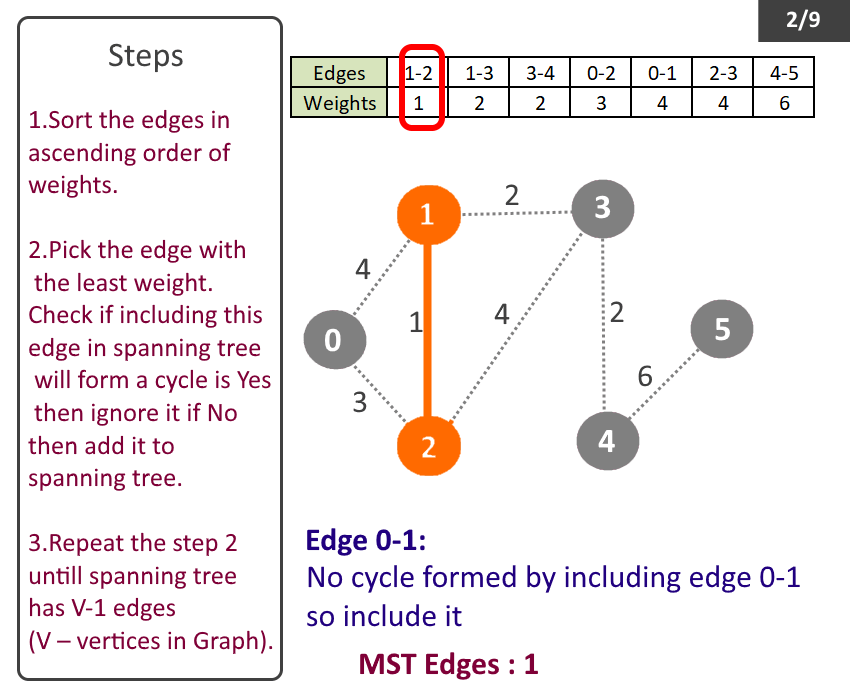
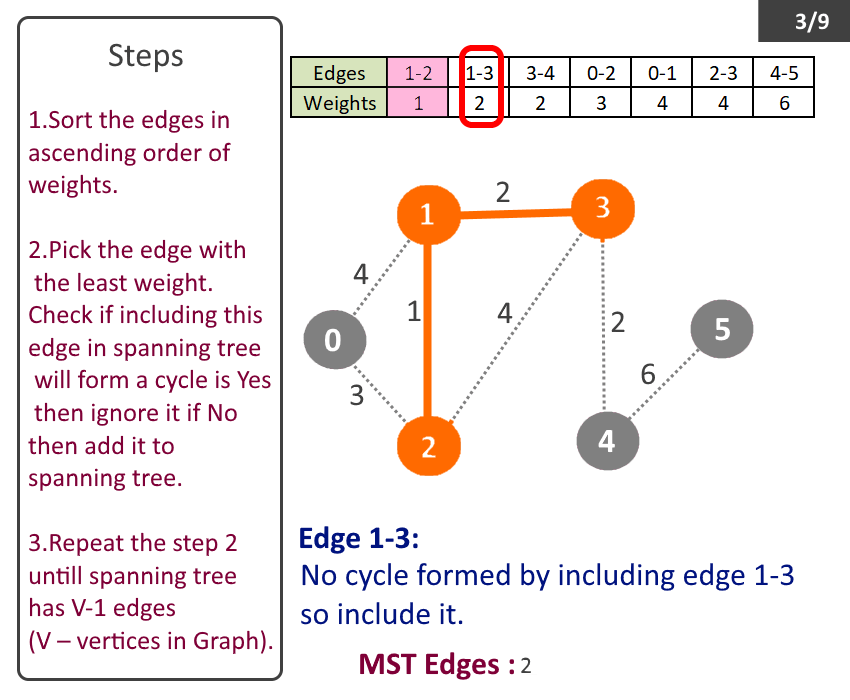
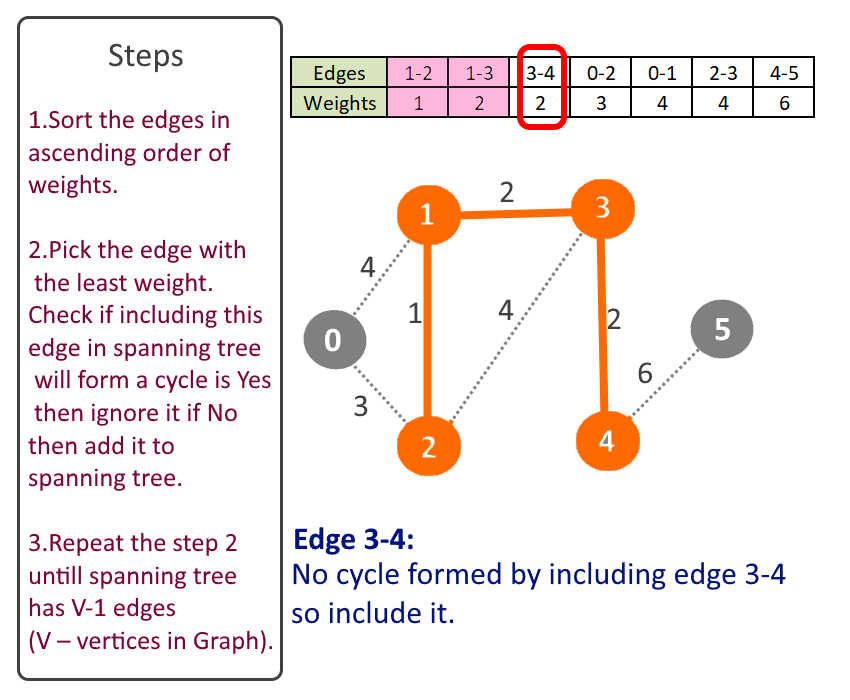
  2. Pick the edge with the least weight. Check if including this edge in spanning tree will form a cycle is Yes then ignore it if No then add it to spanning tree.
  3. Repeat the step 2 till spanning tree has V-1 (V – no of vertices in Graph).
  4. Spanning tree with least weight will be formed, called Minimum Spanning Tree

Pseudo Code:

KRUSKAL(G):
A = ∅
foreach v ∈ G.V:
   MAKE-SET(v)
foreach (u, v) in G.E ordered by weight(u, v), increasing:
   if FIND-SET(u) ≠ FIND-SET(v):
      A = A ∪ {(u, v)}
      UNION(u, v)
return A

See the animation below for more understanding.

Code:


Output:

Minimum Spanning Tree:
Edge-0 source: 1 destination: 2 weight: 1
Edge-1 source: 1 destination: 3 weight: 2
Edge-2 source: 3 destination: 4 weight: 2
Edge-3 source: 0 destination: 2 weight: 3
Edge-4 source: 4 destination: 5 weight: 6

Click here to read about - Minimum Spanning Tree using Prim's Algorithm

Reference - Wiki

Also Read: