|
Be the first user to complete this post
|
Add to List |
129. Binary Min-Max Heap Implementation
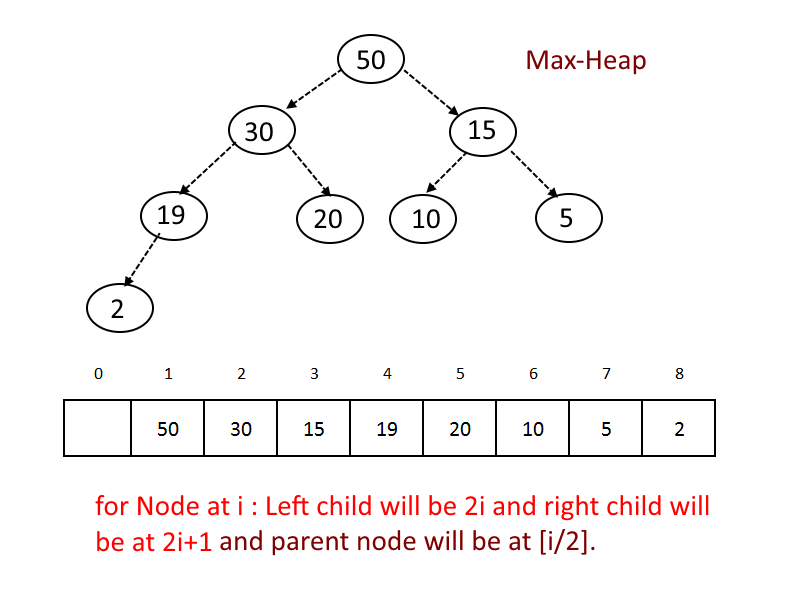
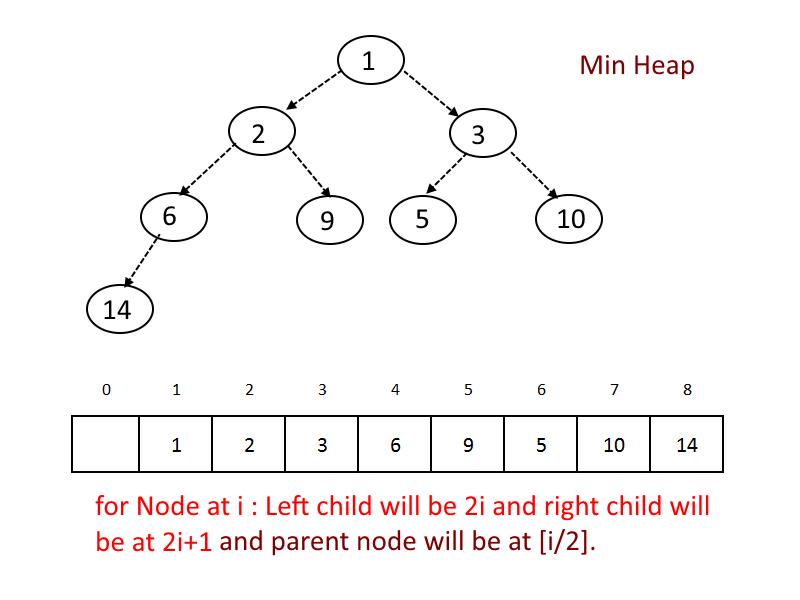
A binary heap is a heap data structure created using a binary tree.
binary tree has two rules -
- Binary Heap has to be a complete binary tree at all levels except the last level. This is called a shape property.
- All nodes are either greater than equal to (Max-Heap) or less than equal to (Min-Heap) to each of its child nodes. This is called heap property.
Implementation:
- Use an array to store the data.
- Start storing from index 1, not 0.
- For any given node at position i:
- Its Left Child is at [2*i] if available.
- Its Right Child is at [2*i+1] if available.
- Its Parent Node is at [i/2]if available.
Heap Majorly has 3 operations -
- Insert Operation
- Delete Operation
- Extract-Min (OR Extract-Max)
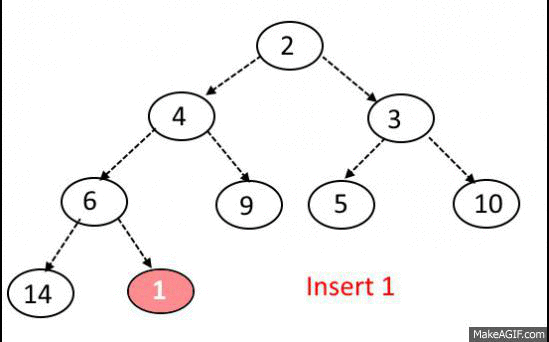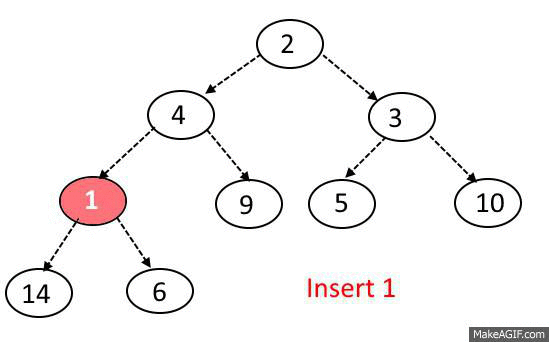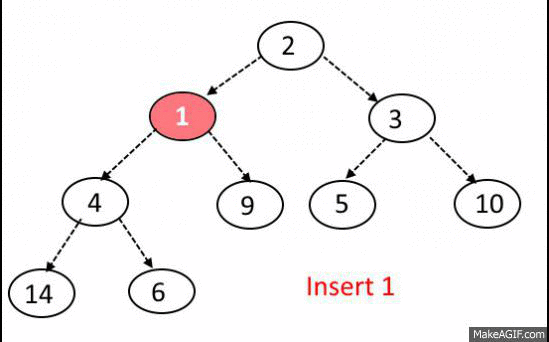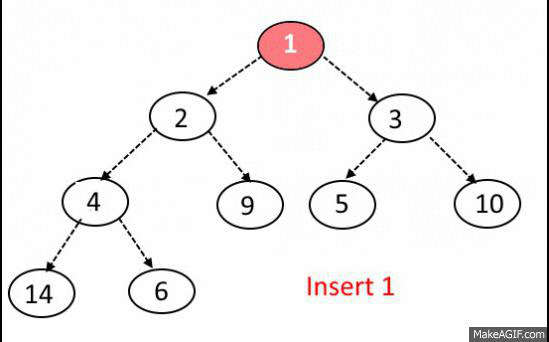
Insert Operation:
- Add the element at the bottom leaf of the Heap.
- Perform the Bubble-Up operation.
- All Insert Operations must perform the bubble-up operation(it is also called as up-heap, percolate-up, sift-up, trickle-up, heapify-up, or cascade-up)
Extract-Min OR Extract-Max Operation:
- Take out the element from the root.( it will be minimum in case of Min-Heap and maximum in case of Max-Heap).
- Take out the last element from the last level from the heap and replace the root with the element.
- Perform Sink-Down
- All delete operations must perform Sink-Down Operation ( also known as bubble-down, percolate-down, sift-down, trickle-down, heapify-down, cascade-down).
Sink-Down Operation:
- If the replaced element is greater than any of its child node in case of Min-Heap OR smaller than any if its child node in case of Max-Heap, swap the element with its smallest child(Min-Heap) or with its greatest child(Max-Heap).
- Keep repeating the above step, if the node reaches its correct position, STOP.
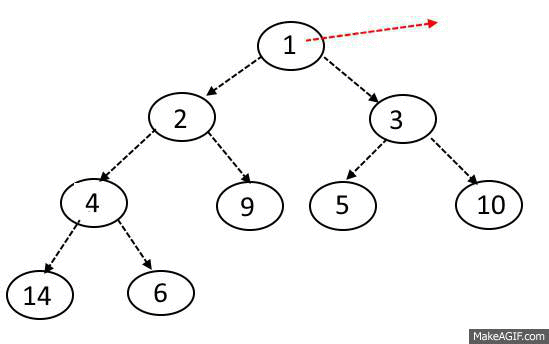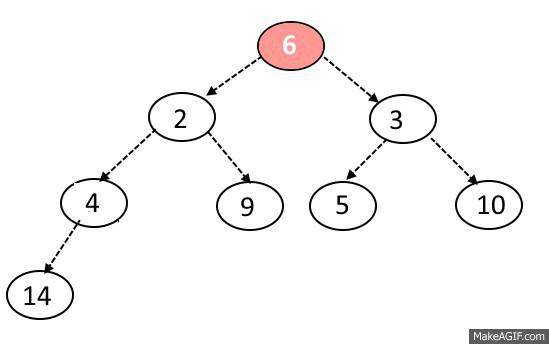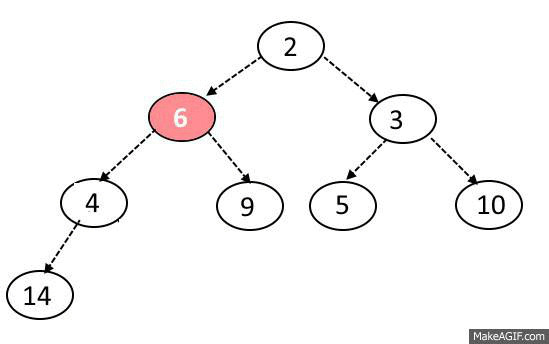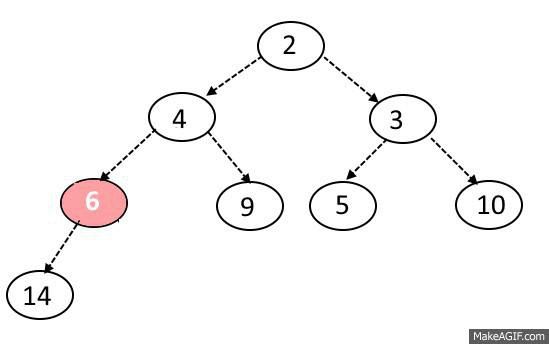
Delete Operation:
- Find the index for the element to be deleted.
- Take out the last element from the last level from the heap and replace the index with this element .
- Perform Sink-Down
Time and Space Complexity:
| Space | O(n) |
| Search | O(n) |
| Insert | O(log n) |
| Delete | O(log n) |
Output:
Original Array : 3 2 1 7 8 4 10 16 12 Min-Heap : 1 3 2 7 8 4 10 16 12 Sorted: 1 3 2 12 8 4 10 16 0

