|
This post is completed by 1 user
|
Add to List |
159. Solve the Knight's Tour with Backtracking
Objective: A knight's tour is a sequence of moves of a knight on a chessboard such that the knight visits every square only once. If the knight ends on a square that is one knight's move from the beginning square (so that it could tour the board again immediately, following the same path), the tour is closed, otherwise, it is open. (Source: http://en.wikipedia.org/wiki/Knight%27s_tour)
Example:
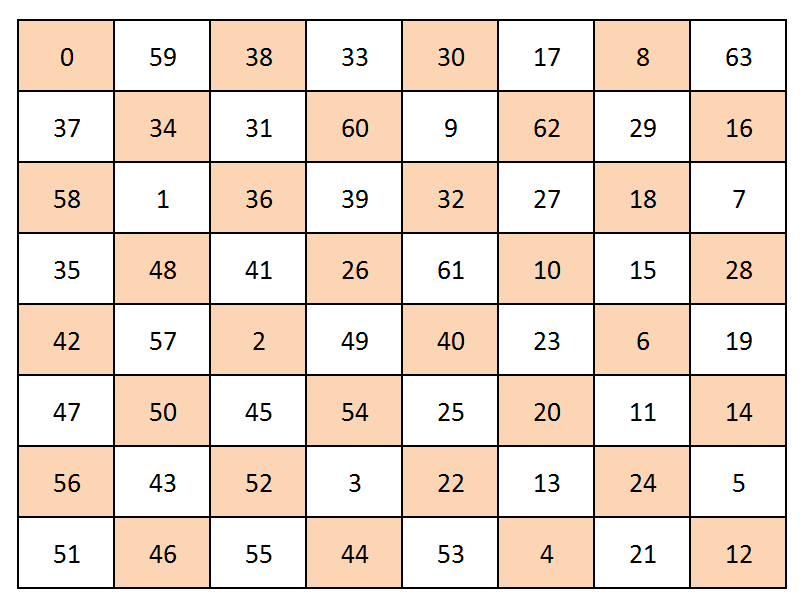
Approach:
- Create a solution matrix of the same structure as a chessboard.
- Start from 0,0 and index = 0. (index will represent the no of cells that the knight has covered)
- Check if the current cell is not already used if not then mark that cell (start with 0 and keep incrementing it, it will show us the path for the knight).
- Check if index = N*N-1 means Knight has covered all the cells. return true and print the solution matrix.
- Now try to solve the rest of the problem recursively by making index +1. Check all 8 directions. (Knight can move to 8 cells from its current position.) Check the boundary conditions as well
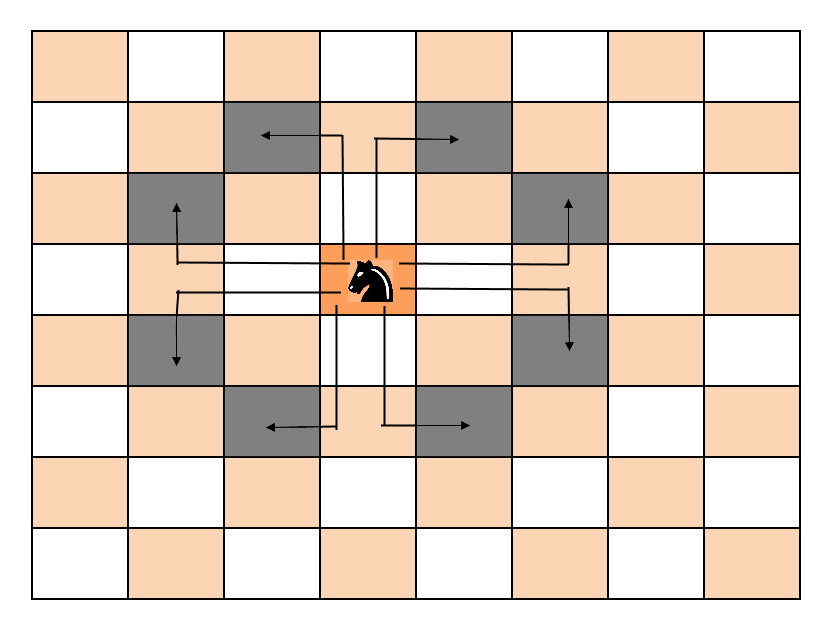
- If none of the 8 recursive calls return true, BACKTRACK and undo the changes ( put 0 to the corresponding cell in the solution matrix) and return false.
- See the code for a better understanding.
Output:
00 59 38 33 30 17 08 63 37 34 31 60 09 62 29 16 58 01 36 39 32 27 18 07 35 48 41 26 61 10 15 28 42 57 02 49 40 23 06 19 47 50 45 54 25 20 11 14 56 43 52 03 22 13 24 05 51 46 55 44 53 04 21 12

