|
This post is completed by 1 user
|
Add to List |
407. Integer Replacement Problem
Objective: Given a number N, write an algorithm to convert that number to 1. Below are the allowed operations.
- If N is even, do N = N/2.
- If N is odd, either do N =N - 1 or do N = N + 1
Example:
N = 16 Output: 4 16 → 8 → 4 → 2 → 1 N = 11 Output: 5 11 → 10 → 5 → 4 → 2 → 1 OR 11 → 12 → 6 → 3 → 2 → 1
Approach: Recursion
- If N is even, then divide it by 2 and add 1 to the result and solve the rest of the problem recursively.
- If N is odd, then solve recursively for both options, N + 1 and N - 1 and pick the one which requires a minimum and adds that to the final result.
- NOTE: when solving for N + 1, do 1 + (n - 1) / 2 and add 2 in result ( to avoid out of range Exception).
Time Complexity: O(2n)
Here we are solving many subproblems repeatedly. See the image below
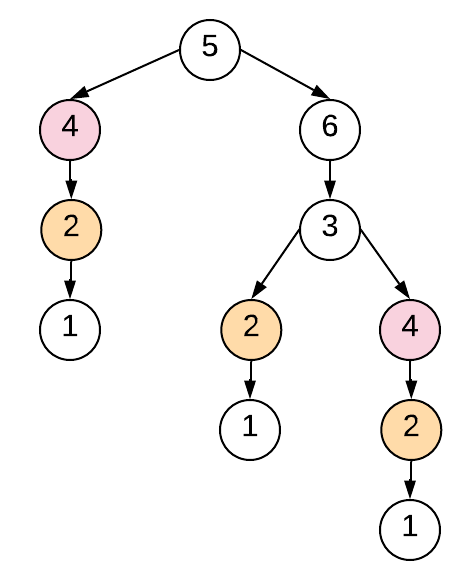
As you can see the for N = 4 and 2, the problem was solved multiple times. We can optimize the solution by using Dynamic Programming.
Dynamic Programming - Top-Down Approach
- Every time we solve recursively for any N, save it in HashMap
- Before solving it for any N, check if we have a solution stored for N in HashMap (means we have already solved it earlier).
Output:
N = 11, Minimum replacements required : 5

