This post is completed by 1 user

  • 0
 Add to List
Hard

162. Dynamic Programming - Subset Sum Problem

Objective: Given a set of positive integers, and a value sum S, find out if there exists a subset in an array whose sum is equal to the given sum S.

Example:

int[] A = { 3, 2, 7, 1}, S = 6

Output: True, subset is (3, 2, 1}

We will first discuss the recursive approach and then we will improve it using Dynamic Programming.

Recursive Approach:

Every element in the array has two options, either we will include that element in the subset or we don't include it.

  • So if we take example as int[] A = { 3, 2, 7, 1}, S = 6
  • If we consider another int array with the same size as A.
  • If we include the element in the subset we will put 1 in that particular index else put 0.
  • So we need to make every possible subset and check if any of the subsets makes the sum as S.
  • If we think carefully this problem is quite similar to " Generate All Strings of n bits"
  • See the code for a better explanation.

Approach: Dynamic Programming (Bottom-Up)

Base Cases:

  • If no elements in the set then we can't make any subset except for 0.
  • If the sum needed is 0 then by returning the empty subset we can make the subset with sum 0.

Given - Set = arrA[], Size = n, sum = S

  • Now for every element in he set we have 2 options, either we include it or exclude it.
  • for any ith element-
  • If include it => S = S-arrA[i], n=n-1
  • If exclude it => S, n=n-1.

Recursive Equation:

Base Cases:
SubsetSum(arrA, n, S)= false, if sum > 0 and n == 0 SubsetSum(arrA, n, S)= true, if sum == 0 (return empty set)
Rest Cases 
SubsetSum(arrA, n, S) = SubsetSum(arrA, n-1, S)|| SubsetSum(arrA, n-1, S-arrA[n-1])
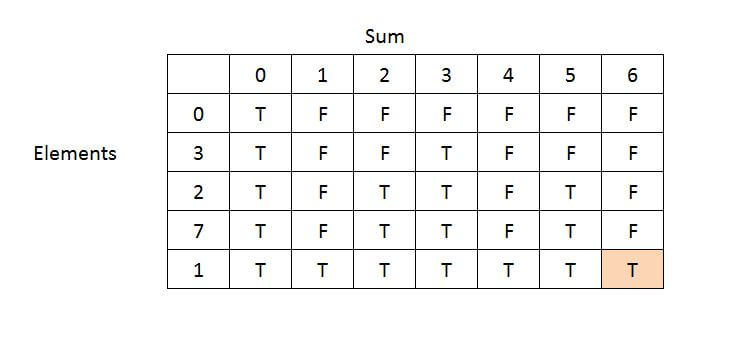
Subset Sum Problem

How to track the elements.

  • Start from the bottom-right corner, backtrack, and check from the True is returning.
  • If the value in the cell above is false, the current cell has become true after including the current element. So include the current element and check for the sum = sum - current element.
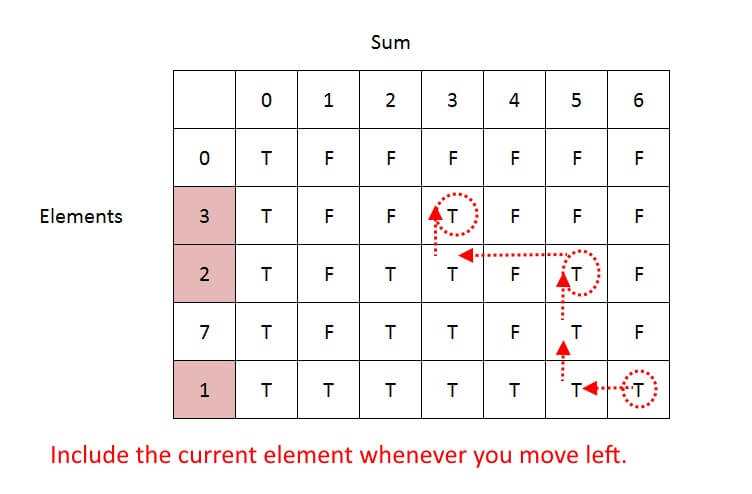
Subset Sum Problem - Track Solution

Output:

Output: From DP: true

Related Problems: