|
This post is completed by 3 users
|
Add to List |
170. Dynamic Programming - Rod Cutting Problem
Objective: Given a rod of length n inches and a table of prices pi, i=1,2,…,n, write an algorithm to find the maximum revenue rn obtainable by cutting up the rod and selling the pieces.
This is a very good basic problem after Fibonacci sequence if you are new to Dynamic programming. We will see how dynamic programming is used to overcome the issues with recursion(Time Complexity).
Given: Rod lengths are integers and For i=1,2,…,n we know the price pi of a rod of length i inches
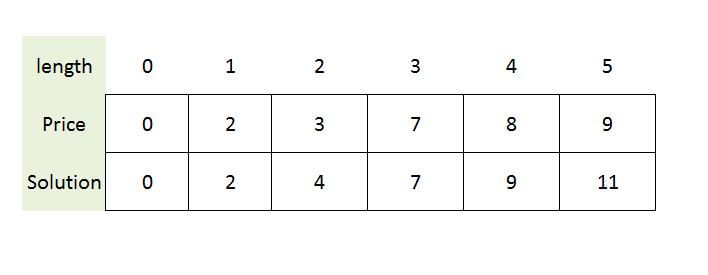
Example:
| Length | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Price | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
for rod of length: 4 Ways to sell : • selling length : 4 ( no cuts) , Price: 9 • selling length : 1,1,1,1 ( 3 cuts) , Price: 4 • selling length : 1,1,2 ( 2 cuts) , Price: 7 • selling length : 2,2 ( 1 cut) , Price: 10 • selling length : 3, 1 ( 1 cut) , Price: 9
Best Price for the rod of length 4: 10
Approach:
Naive Approach: Recursion
- There can be n-1 cuts can be made in the rod of length n, so there are 2n-1 ways to cut the rod.
- So for every length, we have 2 options either we cut it or not. we will consider both options and choose the optimal out of it.
Time Complexity: O(2^n-1)
But this time complexity is very high since we are solving many subproblems repeatedly.
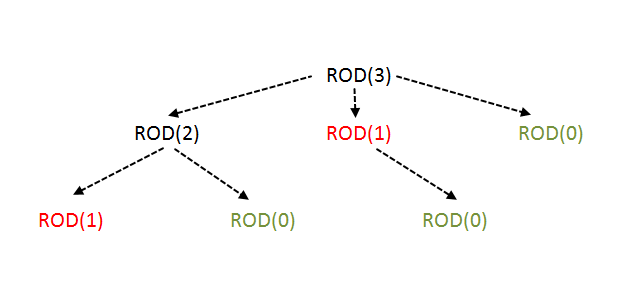
Dynamic Programming: Bottom-Up
Instead of solving the sub-problems repeatedly we can store the results of it in an array and use it further rather than solving them again.
See the Code for a better explanation:
Result: Max profit for length is 5:11