|
This post is completed by 2 users
|
Add to List |
168. Dynamic Programming - Minimum Cost Path Problem
Objective: Given a 2D matrix where each cell has a cost to travel. You have to write an algorithm to find a path from the left-top corner to the bottom-right corner with minimum travel cost. You can move only right or down.
In the solution, we will see how dynamic programming is a much better approach than recursion.
Example:
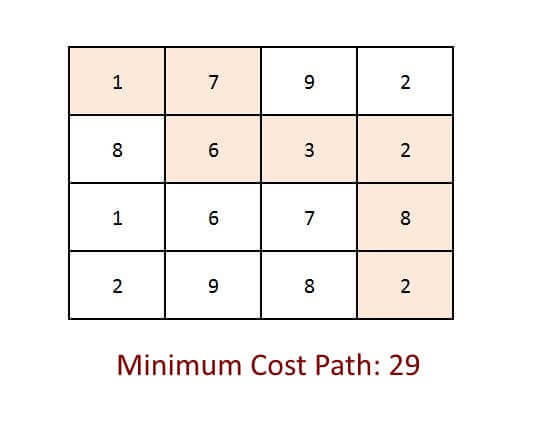
Approach:
This problem is similar to Find all paths from top-left corner to bottom-right corner.
We can solve it using Recursion ( return Min(path going right, path going down)) but that won't be a good solution because we will be solving many sub-problems multiple times. Since at every cell we have 2 options the time complexity will be O(2n).
Dynamic Programming:
Create a solution matrix of the same size as a given matrix.
We will fill this matrix in Bottom-up manner.
Given: arrA[][].
At every cell, we have two options (go right or down) and we will choose the minimum of these two. So for any i,j cell solution[i][j] = A[0][j] if i=0 , first row = A[i][0] if j=0, first column = A[i][j] + Min(solution[i-1],[j] , solution[i][j-1]) if i>0 && j>0 See the code for better Explanation.
Time Complexity: O(n2).
Output
Minimum Cost Path 29

