|
This post is completed by 1 user
|
Add to List |
200. Dynamic Programming - Highway Billboard Problem
Objective: Suppose you’re managing the construction of billboards on the Rocky & Bullwinkle Memorial Highway, a heavily traveled stretch of road that runs west-east for M miles. The possible sites for billboards are given by numbers x1 < x2 < · · · < xn, each in the interval [0, M], specifying their position in miles measured from the western end of the road. If you place a billboard at position xi, you receive revenue of ri > 0.
Regulations imposed by the Highway Department require that no two billboards be within five miles or less of each other. You’d like to place billboards at a subset of the sites so as to maximize your total revenue, subject to this restriction.
Problem Source: https://cgi.csc.liv.ac.uk/~martin/teaching/comp202/Exercises/Dynamic-programming-exercises-solution.pdf
Example:
int[] x = {6, 7, 12, 13, 14};
int[] revenue = {5, 6, 5, 3, 1};
int distance = 20;
int milesRestriction = 5;
Output: Maximum revenue can be generated :10 ( x1 and x3 billboard will be placed)
Approach:
We will solve this problem using dynamic programming in a bottom-up manner.
let's say
"MR(i) is Maximum Revenue generated for i miles in highway"
Now for each mile on the highway, we need to check whether this mile has an option for any billboard, if not then the maximum revenue generated till that mile would be the same as the maximum revenue generated one mile before.
But if that mile has an option for a billboard then we have 2 options
- Either we will place the billboard (ignore the billboards in the previous 5 miles) and add the revenue of the billboard placed.
- OR we will ignore the billboard
So we will choose the option which will generate the maximum revenue.
MR(i) = Max{MR(i-6) + Revenue[i], MR[i-1]}
Note: Two billboards has to be more than 5 miles away so actually we add MR(i-6) with revenue
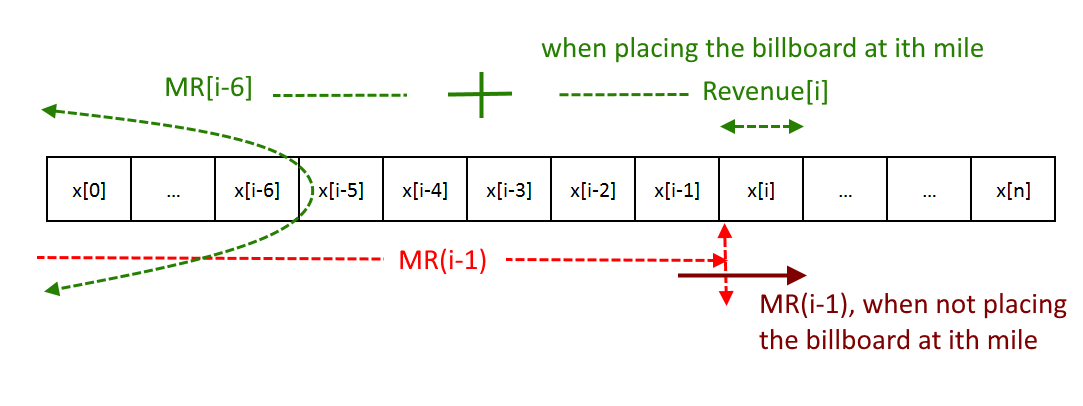
Read the code for more understanding.
Output:
[0, 0, 0, 0, 0, 0, 5, 6, 6, 6, 6, 6, 10, 10, 10, 10, 10, 10, 10, 10, 10] Maximum revenue can be generated:10
Track the actual solution: To track the actual solution use MR[]. Start traversing from the end to the start. Whenever value changes mean a billboard has been placed at the location. Note the billboard and jump 5 miles back (no two billboards be within five miles or less of each other) and again traverse backward and so on.


