This post is completed by 2 users

  • 0
 Add to List
Medium

447. Check If Given Undirected Graph is a tree

Objective: Given an undirected graph, Write an algorithm to determine whether it is a tree or not.

An undirected graph is a tree if it has the properties mentioned below

  1. There is no cycle present in the graph.
  2. The graph is connected. (All the vertices in the graph are connected)

Example:

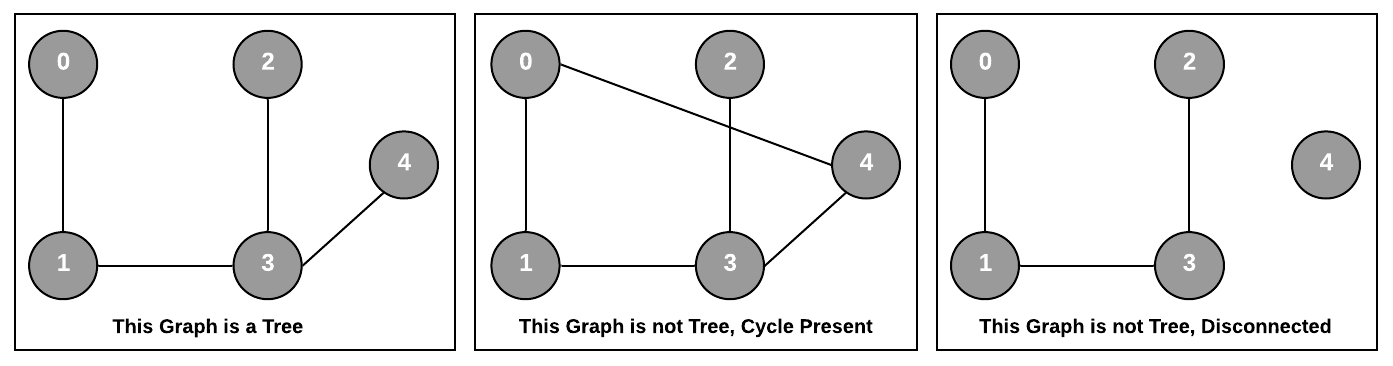
Recommended articles to read before continue reading

  1. Detect Cycle in an Undirected Graph using DFS.
  2. Check if Given Directed Graph is disconnected

Approach: 

Do DFS from any vertex. (please read DFS here), During DFS, for any current vertex X (currently visiting vertex) if there an adjacent vertex Y is present which is already visited and Y is not a direct parent of X then there is a cycle in the graph. If Cycle is present that means the graph is not a tree. If the cycle is not present then check whether the graph is connected. No need to do the DFS again to determine that, use the visited[] array filled during checking the cycle, if all the vertices are true in visited[] array means graph is connected and the graph is a tree else the graph is not the tree.  

 

Output:

Vertex connected from vertex: 0
->1
Vertex connected from vertex: 1
->3->0
Vertex connected from vertex: 2
->3
Vertex connected from vertex: 3
->4->2->1
Vertex connected from vertex: 4
->3
Given Graph is Tree
----------------------------
Vertex connected from vertex: 0
->4->1
Vertex connected from vertex: 1
->3->0
Vertex connected from vertex: 2
->3
Vertex connected from vertex: 3
->4->2->1
Vertex connected from vertex: 4
->0->3
Given Graph is not Tree
----------------------------
Vertex connected from vertex: 0
->1
Vertex connected from vertex: 1
->3->0
Vertex connected from vertex: 2
->3
Vertex connected from vertex: 3
->2->1
Vertex connected from vertex: 4

Given Graph is not Tree

Reference: GeeksforGeeks

Related Problems: