Binary tree traversal
Problem description :
Tree traversal (a.k.a tree search) is a form of graph traversal and refers to the process of visiting each node in a tree data structure, exactly once, in a systematic way. Such traversals are classified by the order in which the nodes are visited. Most commonly used traversal orders are the following :
- In-order
- Pre-order
- Post-order
This post is a follow-up of Create a binary search tree in javascript. I recommend reading that first, as the following code uses the method from it.
Time complexity : O(n); n is the number of nodes in a tree
Pre-order traversal :
- Display the data part of root element (or current element)
- Traverse the left subtree by recursively calling the pre-order function.
- Traverse the right subtree by recursively calling the pre-order function
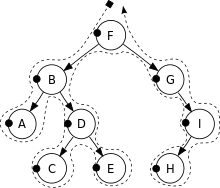
Pre-order: F, B, A, D, C, E, G, I, H
Solution :
In-order traversal :
- Traverse the left subtree by recursively calling the in-order function
- Display the data part of root element (or current element)
- Traverse the right subtree by recursively calling the in-order function
Note: Elements are printed in the sorted order.
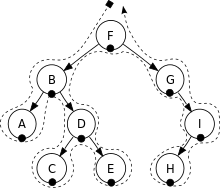
In-order: A, B, C, D, E, F, G, H, I
Solution :
Post-order traversal :
- Traverse the left subtree by recursively calling the post-order function.
- Traverse the right subtree by recursively calling the post-order function.
- Display the data part of root element (or current element).
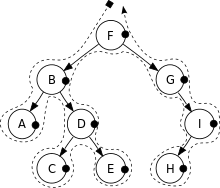
Post-order: A, C, E, D, B, H, I, G, F

