Be the first user to complete this post

  • 0
 Add to List
Hard

335. Max Flow Problem – Introduction

Max Flow Problem-

  • Maximum flow problems find a feasible flow through a single-source, single-sink flow network that is maximum.
  • This problem is useful for solving complex network flow problems such as the circulation problem.
  • The maximum value of the flow (say the source is s and sink is t) is equal to the minimum capacity of an s-t cut in the network (stated in max-flow min-cut theorem).
  • In maximum flow graph, Incoming flow on the vertex is equal to outgoing flow on that vertex (except for source and sink vertex)

Example:

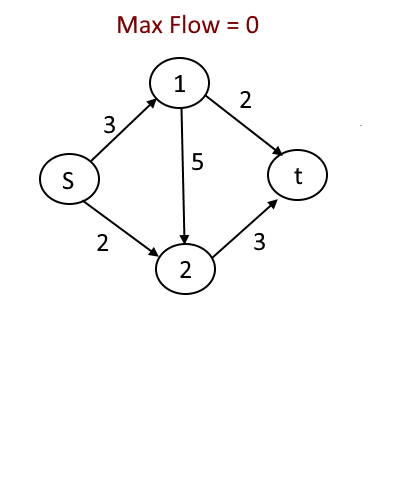
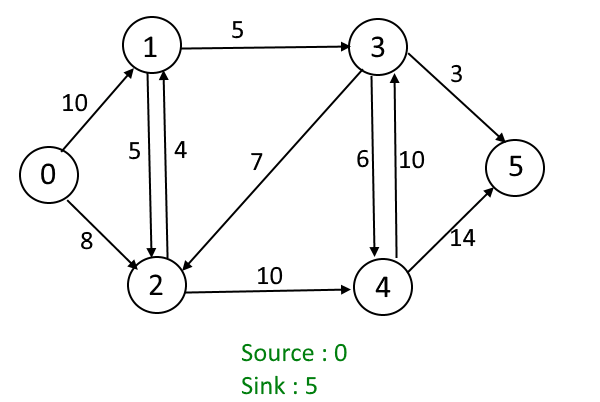
Max flow example

Given the graph, each edge has a capacity (the maximum unit can be transferred between two vertices). Find out the maximum flow which can be transferred from source vertex (S) to sink vertex (T).

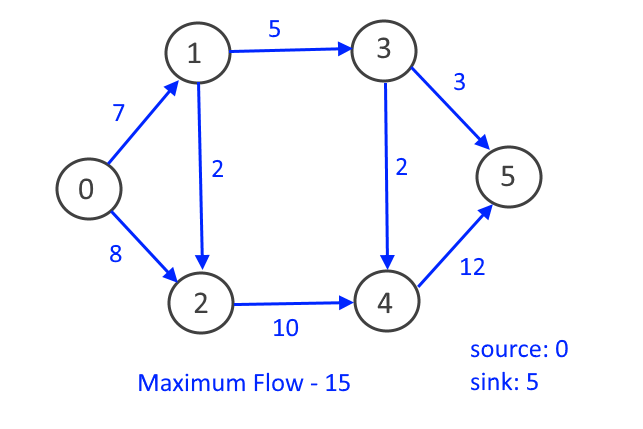
Max Flow Example

Greedy Approach:

This approach may not produce the correct result but we will modify the approach later.

  1. Max_flow = 0
  2. Use BFS or DFS to find the paths.
  3. While(Path exist from source(s) to destination(t) with capacity > 0)
    • Find the minimum_flow (minimum capacity among all edges in path).
    • Add minimum_flow  to the Max_Flow.
    • Reduce the capacity of each edge by minimum_flow.
  4. Return Max_flow.

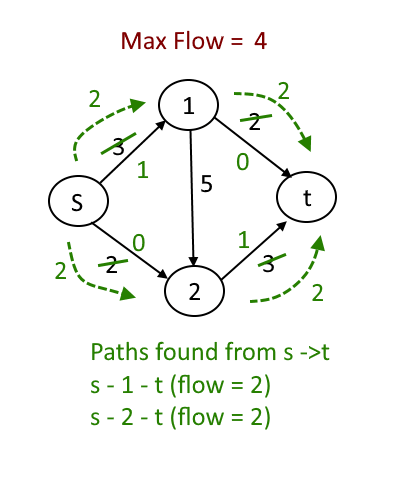
Let’s understand it better by an example

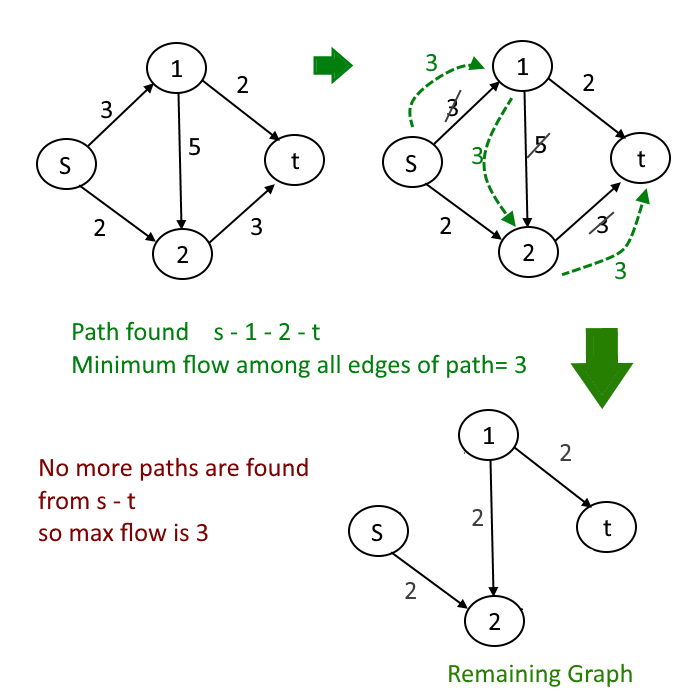
  1. Choose path S-1-2-t first

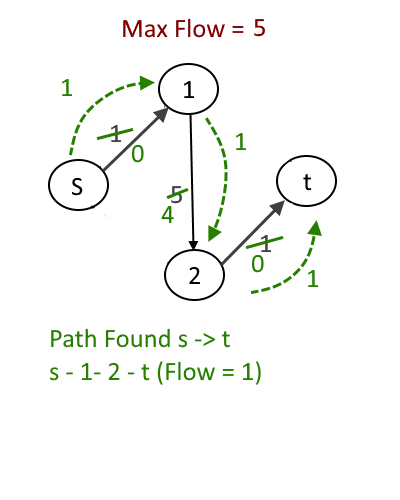
Now let’s take the same graph but the order in which we will add flow will be different. See the animation below.

  • Choose path S-1-2-t later

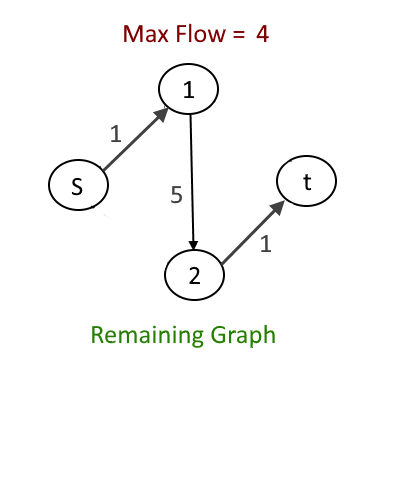
Now as you can clearly see just by changing the order the max flow result will change. The correct max flow is 5 but if we process the path s-1-2-t before then max flow is 3 which is wrong but greedy might pick s-1-2-t .  That is why greedy approach will not produce the correct result every time.

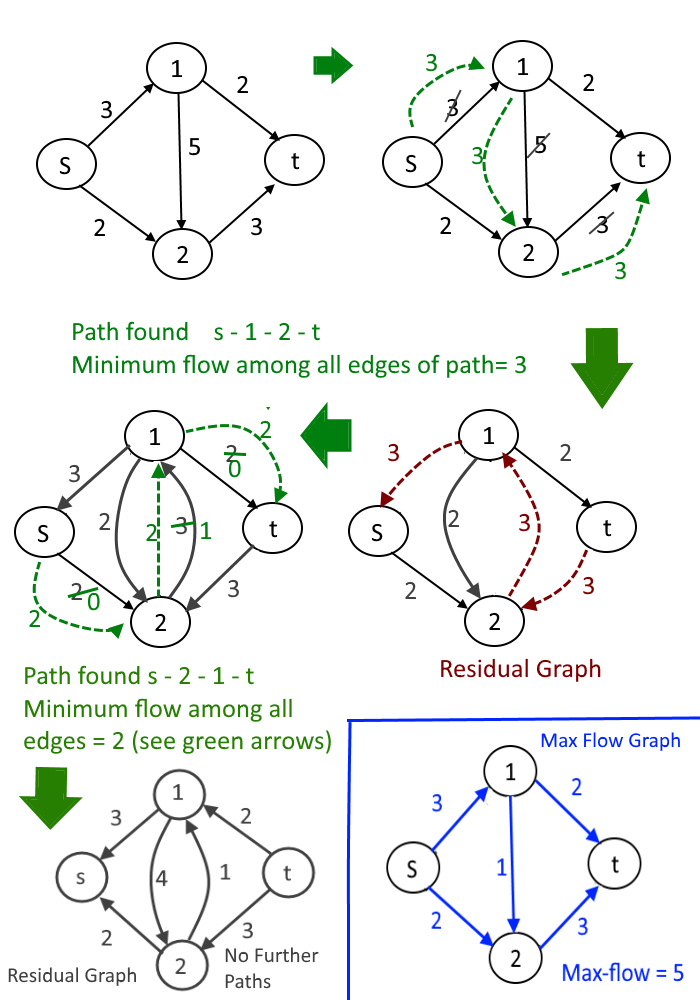
We will use Residual Graph to make the above algorithm work even if we choose path s-1-2-t.

Residual Graph:

The second idea is to extend the naive greedy algorithm by allowing “undo” operations. For example, from the point where this algorithm gets stuck (Choose path s-1-2-t first, our first approach), we’d like to route two more units of flow along the edge (s, 2), then backward along the edge (1, 2), undoing 2 of the 3 units we routed the previous iteration, and finally along the edge (1, t). This would yield the maximum flow, same as (Choose path s-1-2-t later, our second approach)

See the approach below with a residual graph.

We need a way of formally specifying the allowable “undo” operations. This motivates the following simple but important definition, of a residual network. The idea is that, given a graph G and a flow f in it, we form a new flow network Gf that has the same vertex set of G and that has two edges for each edge of G. An edge e = (v, w) of G that carries flow fe and has capacity ue (Image below) spawns a “forward edge” (u, v) of Gf with capacity ue −fe (the room remaining)and a “backward edge” (w, v) of Gf with capacity fe (the amount of previously routed flow that can be undone)

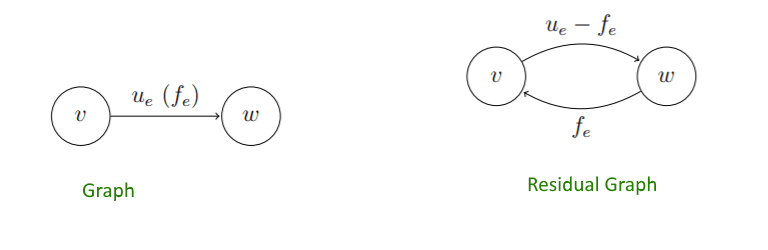
Further, we will implement the Max flow Algorithm using Ford-Fulkerson

Reference: Stanford Edu and GeeksForGeeks

Related Problems: